Презентация к уроку "нахождение площади фигур" - "формула пика". По математике на тему "Формула Пика"

Библиографическое описание: Татьяненко А. А., Татьяненко С. А. Вычисление площадей фигур, изображенных на клетчатой бумаге // Юный ученый. 2016. №3..03.2019).

При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?

Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.

Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.

Возможны следующие случаи.

1. Фигура представляет собой треугольник, параллелограмм, трапецию:

1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;

2) подставить найденные величины в формулу площади.

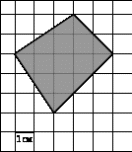
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.

Рис. 1. Треугольник

Решение. Подсчитываем клеточки и находим: . По формуле получаем: .

2 Фигура представляет собой многоугольник

Если фигура представляет собой многоугольник то возможно использовать следующие методы.

Метод разбиения:

1) разбить многоугольник на треугольники, прямоугольники;

2) вычислить площади полученных фигур;

3) найти сумму всех площадей полученных фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.

Рис. 2. Многоугольник

Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.

Рис. 3. Многоугольник. Метод разбиения

Площади треугольников равны: , , , площадь прямоугольника - . Складывая площади всех фигур получим:

Метод дополнительного построения

1) достроить фигуру до прямоугольника

2) найти площади полученных дополнительных фигур и площадь самого прямоугольника

3) из площади прямоугольника вычесть площади всех «лишних» фигур.

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.

Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.

Рис. 4. Многоугольник. Метод дополнения

Площадь большого прямоугольника равна , прямоугольника, расположенного внутри - , площади «лишних» треугольников - , , тогда площадь искомой фигуры .

При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.

Формула Пика

Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.

Площадь многоугольника с целочисленными вершинами равна , где B - количество целочисленных точек внутри многоугольника, а Г - количество целочисленных точек на границе многоугольника.

Например, для многоугольника, изображенного на рисунке 5.

Рис. 5. Узлы в формуле Пика

Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.

Рис. 6. Многоугольник. Формула Пика

Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:

Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.

1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.

Рис. 7. Условие задачи 1

2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых - до 35 т, вяза - до 43 т, дуба - до 50 т. бука - до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. - 200 м.).

Рис. 8. Условие задачи 2

3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.

Рис. 9. Условие задачи 3

4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см - 5м.

Рис. 10. Условие задачи 4

5. Звездчатый многоугольник - плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда - пентаграмма. Пентаграмма - это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.

Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее - метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.

Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.

Литература:

Вавилов В. В., Устинов А. В. Многоугольники на решетках. - М.: МЦНМО, 2006. - 72 с.
Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». - 1974. - № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. - 2009. -№ 23. - с.24,25.

Просмотр содержимого документа
«На выступление»

Введение

Рано или поздно всякая правильная

математическая идея находит

(А.Н. Крылов)

Многие ученики сталкиваются с задачами на нахождение площади треугольника, параллелограмма, многоугольника и других геометрических фигур по рисунку на клетчатой бумаге. Применяя правила и теоремы из геометрии, ученик может запутаться или забыть, да и к тому же уходит много времени на дополнительное построение, а в условиях экзамена дорога каждая минута. Чтобы не тратить много усилий, времени и не вспоминать впопыхах теоремы, аксиомы, правила, существует теорема Пика, с помощью которой можно без проблем и траты времени вычислить площадь фигуры, расположенной на клетчатой бумаге.

Увидев такие задачи в контрольно–измерительных материалах ОГЭ и ЕГЭ, решил обязательно исследовать задачи на клетчатой бумаге, связанные с нахождением площади изображённой фигуры.

Так и была определена тема для исследования.

Теорема Пика актуальна для всех школьников, сдающих экзамены. Поэтому её нужно знать, чтобы быстро и правильно решать задачи на нахождение площади.
Объект исследования : задачи на клетчатой бумаге.

Предмет исследования : задачи на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Методы исследования :

Теоретические: анализ и синтез.

Эмпирические: сравнение.
Индуктивный метод – получение выводов из конкретных примеров.

Эксперимент.

Цель исследования: Проверить формулу Пика для вычисления площадей геометрических фигур в сравнении с формулами геометрии.

А кто же такой Пик?

Пик поступил в университет в Вене в 1875 году. Уже в следующем году он опубликовал свою первую работу по математике, ему было всего лишь семнадцать лет. Он изучал математику и физику, окончил в 1879 г. универститет, получив возможность преподавать оба эти предмета. В 1877 году из Дрезденской Высшей технической школы (Technische Hochschule) переехал Лео Кёнигсбергер, который занял кафедру в венском университете. Он стал руководителем Пика, и 16 апреля 1880 г. Пик защитил докторскую диссертацию “О классе абелевых интегралов”

Формула Пика позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.

Это задание мы рассматривали на уроке. Хотя многоугольник выглядел достаточно просто, для вычисления его площади нам пришлось изрядно потрудиться. Мы потратили 10 минут времени на решение этой задачи. Хочу отметить, что не все учащиеся нашего класса справились с данным заданием. А когда нам сказали, что есть формула позволяющая вычислить площадь за одну минуту, то меня очень заинтересовало и я решил заняться изучением этого вопроса.

Сначала я решил узнать какими способами вычисляли площадь мои одноклассники, кто справился с заданием и заняться изучением формулы. В нашем классе никто не знал формулы Пика. Также это задание мы решили дать учащимся 9 и 11 классов. Вот что у нас получилось.

Формула Пика:

А сейчас мы хотели показать вам пример, как с помощью формулы Пика можно найти площадь фигуры на клетчатой решетки.

Вывод: Таким образом, рассматривая задачи на нахождение площадей многоугольников, изображенных на клетчатой бумаге, по формулам геометрии и по формуле Пика и сравнивая результаты в таблицах, мы показали справедливость формулы Пика и пришли к выводу, что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по выведенной формуле геометрии.

«Формула Пика»

Выполнил:

Руководитель: Паркина Наталья Ивановна,

учитель математики

Актуальность

Объект исследования:

Задачи на клетчатой бумаге.

Предмет исследования:

Методы исследования:

Цель исследования:

применение в том или ином деле.

(А.Н. Крылов)

Подсчет количества клеток;
Формула Пика.

Найдём площадь многоугольника

Искать её можно по-разному.

S = 5 ・ 6 – 13=17 (кв.ед.)

Вот что у нас получилось

Класс

Правильно

Неправильно

всего

Способ

Класс

Подсчет клеток

Разбиение фигуры

всего

Формула

Пика

Теорема Пика или Формула Пика

Пусть В −

Г − S − его площадь.

S = В + Г/2 – 1

Пример.

В = 13 (красные точки),

Г= 6 (синие точки), поэтому

S = 13 + 6/2 – 1 = 15 квадратных единиц.

Доказательство

Обозначим:

сторонах,

Следовательно, площадь многоугольника равна 1/2 m .

180 0 m .

180 0 (Г – n ).

n – 2) .

Общая сумма углов всех треугольников равна

360 0 В +180 0 (Г– n ) + 180 0 (n –2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г– n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 , 1/2 m = В + Г/2 – 1 ,

Г=4(точки на узлах)

В=0(точки внутри фигуры)

Ответ: 1см 2

1 клетка = 1 см
Г = 15 (обозначены красным)
В = 34 (обозначены синим)

Г = 14 (обозначены красным)
В = 43 (обозначены синим)

Решение заданий ЕГЭ

Формула Пика-

формула для вычисления

площади

многоугольников,

полезна при решении заданий

ЕГЭ и ОГЭ

Задание ЕГЭ – 2015

Решение.

По формуле Пика:

S = Г:2 + В - 1

Г = 7 , В = 5

S = 7:2 + 5 – 1 =

= 7,5 (см²)

Ответ: 7,5 см².

Задания ЕГЭ - 2015

Г = 7 В = 2

S = 7:2 + 2 - 1 = 4 ,5

Г = 4 В = 0

S = 4: 2 + 0 - 1 = 1

Задача. Найдите площадь S

Ответ: ≈ 1,11.

Задача . ABC .

Задача. ABCD

Задача. Найдите площадь S

Ответ: ≈3,5.

Пример №1

Г = 14

S = 14:2 + 43–1 =

= 49

Пример № 2

Г = 11

S = 11:2 + 5 – 1= = 9,5

Пример №3

S = 15:2 + 22 – 1=

Пример № 4

S = 8:2 +16 – 1 =

Пример № 5

Г = 10

S = 10:2 + 30 –1 =

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

По формуле Пика S =В +½Г-1 В=4,Г=14, S=4+½·14-1=10

По формуле Пика S =В +½Г-1 В=36, Г=21

По формуле Пика S =В +½Г-1 В=36, Г=21 S = 36 + ½·21 -1=36+10,5-1=45,5

По формуле Пика S =В +½Г-1 В=6,Г=18, S=6+½·18-1=14

Г = 16 В = 4 S = Г : 2 + В - 1 S = 16 : 2 + 4 – 1 = 11

Задача.

Основной вывод:

Заключение

Просмотр содержимого презентации
«Формула Пика2»

Исследовательская работа по математике

Применение формулы Пика для вычисления площади многоугольников с вершинами в узлах клетки

Выполнил: Васякин Михаил, ученик 10 класса

Руководитель: Паркина Наталья Ивановна,

учитель математики

Актуальность работы состоит в том, что формула Пика для вычисления площади многоугольников в школьном курсе математики (геометрии) не рассматривается. Изучение данной темы расширяет интеллектуальный кругозор учащихся, а применение её упрощает нахождение площади геометрической фигуры, изображенной на клетчатой бумаге (сетке). Контрольно-измерительные материалы ЕГЭ содержат задания подобного типа, и их можно решить, применяя формулу Пика.

Объект исследования:

Задачи на клетчатой бумаге.

Предмет исследования:

Задачи на вычисление площади многоугольника на клетчатой бумаге.

Методы исследования:

Сравнение, моделирование, обобщение, аналогии, изучение литературы и Интернет-ресурсов, анализ и классификация информации.

Цель исследования:

Обосновать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.

Изучить литературу по данной теме;
Рассмотреть различные способы вычислений площадей многоугольников;
Показать практическое применение этих способов;
Выяснить преимущества и недостатки каждого способа;
Систематизировать и углубить накопленные мной знания;
Повысить качество знаний и умений;
Создать электронную презентацию работы для представления собранного материала одноклассникам.

Рано или поздно всякая правильная математическая идея находит

применение в том или ином деле.

(А.Н. Крылов)

Георг Александр Пик- австрийский математик, родился в еврейской семье.

Круг математических интересов Пика был чрезвычайно широк. Им написаны работы в области математического анализа, дифференциальной геометрии, в теории дифференциальных уравнений и т. д., всего более 50 тем.

Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.

Подсчет количества клеток;
Применение формул планиметрии;
Разбиение фигуры на более простые фигуры;
Достроение фигуры до прямоугольника;
Формула Пика.

Найдём площадь многоугольника

Искать её можно по-разному.

Способы, применяемые для вычисления площади данной фигуры

1способ: Подсчет количества клеток (для данной фигуры приближенный).

2 способ: Попробовать разрезать многоугольник на достаточно простые фигуры (рис.2), найти их площади и сложить.

3 способ: Вычислить площадь фигуры (рис.3), которая дополняет многоугольник до прямоугольника, и вычесть эту площадь из площади прямоугольника. Дополненная фигура (в отличие от исходного многоугольника) легко разбивается на прямоугольники и прямоугольные треугольники так, что её площадь вычисляется без усилий.

S = 2+1+0,5 + 3+ 2 + 1 + 2 +1,5=13 (кв.ед.)

Следовательно, площадь исходного многоугольника равна

S = 5 ・ 6 – 13=17 (кв.ед.)

Вот что у нас получилось

Класс

Правильно

Неправильно

всего

Способ

Подсчет клеток

Класс

Разбиение фигуры

всего

Достроить фигуру до прямоугольника

Формула

Пика

Попробуйте найти площадь фигуры

Для этого есть простой и удобный способ.

Теорема Пика или Формула Пика

Пусть В − число узлов сетки внутри многоугольника,

Г − количество узлов на его границе, S − его площадь.

Тогда справедлива формула Пика: S = В + Г/2 – 1

Пример.

Для многоугольника на рисунке В = 13 (красные точки),

Г= 6 (синие точки), поэтому

S = 13 + 6/2 – 1 = 15 квадратных единиц.

Доказательство

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах

решётки, не содержащие узлов ни внутри, ни на

сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны

Следовательно, площадь многоугольника равна 1/2m.

Общая сумма углов всех треугольников равна 180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна

180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна

360 0 В +180 0 (Г– n ) + 180 0 (n –2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г– n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 , 1/2m= В + Г/2 – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + Г/2 – 1 , известное как формула Пика.

Г=4(точки на узлах)

В=0(точки внутри фигуры)

Ответ: 1см 2

1 клетка = 1 см
Г = 15 (обозначены красным)
В = 34 (обозначены синим)

Г = 14 (обозначены красным)
В = 43 (обозначены синим)

Решение заданий ЕГЭ

Формула Пика-

формула для вычисления

площади

многоугольников,

полезна при решении заданий

ЕГЭ и ОГЭ

Задание ЕГЭ – 2015

Найдите площадь четырёхугольника АВСD

Решение.

По формуле Пика:

S = Г:2 + В - 1

Г = 7 , В = 5

S = 7:2 + 5 – 1 =

= 7,5 (см²)

Ответ: 7,5 см².

Задания ЕГЭ - 2015

Г = 7 В = 2

S = 7:2 + 2 - 1 = 4,5

Г = 4 В = 0

S = 4: 2 + 0 - 1 = 1

Теперь, зная новую формулу, мы легко сможем найти площадь и этого четырехугольника.

Так как В =5; Г = 14, то 5+14:2-1=11 (см в квадрате)

Площадь данного четырехугольника равна 11 см в квадрате.

По той же формуле мы можем найти площадь треугольника.

Так как В=14, Г=10,то 14+10:2-1=18 (см в квадрате)

Площадь данного треугольника равна 18 см в квадрате.

Если В=9, Г=12, тогда: 9+12:2-1=14 (см в квадрате)

Площадь данного четырехугольника равна 14 см в квадрате.

Задача. Найдите площадь S сектора, считая стороны квадратных клеток равными 1. В ответе укажите.

Решение: Г= 5, В= 2, S = В + Г/2 – 1= 2 + 5/2 – 1= 3,5 .

Ответ: ≈ 1,11.

Задача . Найдите площадь треугольника ABC .

Решение: Г = 7, В = 5, S = В + Г/2 – 1= 5 + 7/2 – 1= 7,5.

Задача. Найдите площадь четырехугольника ABCD , считая стороны квадратных клеток равными 1.

Решение: Г= 4, В= 5, S = В + Г/2 – 1= 5 + 4/2 – 1= 6

Задача. Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите

Решение: Г= 8, В= 8, S = В + Г/2 – 1= 8 + 8/2 – 1=11,

Ответ: ≈3,5.

Пример №1

Г = 14

S = 14:2 + 43–1 =

Пример №2

Г = 11

S = 11:2 + 5 – 1= = 9,5

Пример №3

S = 15:2 + 22 – 1=

Пример № 4

S = 8:2 +16 – 1=

Пример № 5

Г = 10

S = 10:2 + 30 –1=

По формуле Пика S =В +½Г-1 В=4,Г=14, S=4+½·14-1=10

По формуле Пика S =В +½Г-1 В=36, Г=21

S = 36 + ½·21 -1=36+10,5-1=45,5

По формуле Пика S =В +½Г-1 В=6,Г=18, S=6+½·18-1=14

Г = 16 В = 4 S = Г : 2 + В - 1 S = 16 : 2 + 4 – 1 = 11

Задача. Найти площадь прямоугольного параллелепипеда, считая стороны квадратных клеток равными 1.

полной поверхности по формуле Пика невозможно!

Основной вывод:

Формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:

1.Для вычисления площади многоугольника, нужно знать всего одну формулу: S = В + Г/2 - 1

2.Формула Пика очень проста для запоминания.

3.Формула Пика очень удобна и проста в применении.

4.Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.

Заключение

При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге двумя способами: геометрическим и с помощью формулы Пика.

Проанализировав способы решения задач, можно сделать следующие выводы:

1) Формула Пика даёт быстрое и простое решение задач на нахождение площади фигуры, вершины которой лежат в узлах решётки, то есть нахождения площадей многоугольников.

2) Использование формулы Пика для нахождения площади кругового сектора или кольца нецелесообразно, так как она даёт приближённый результат.

3) Формула Пика не применяется для решения задач в пространстве.

4) Формула Пика облегчает и ускоряет нахождение площади многоугольников. Но и она имеет свои недостатки:

Чертёж должен быть очень четким (для подсчета узлов);
Формула применяется лишь в том случае, если многоугольник изображен на клетчатой бумаге;

Способы вычисления площадей многоугольников, в том числе с помощью формулы Пика позволяет успешному изучению геометрии в старших классах. Данная работа может быть полезна для учащихся при подготовке к итоговой аттестации.

При помощи формулы Пика можно находить площадь фигуры, построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник).

В задачах, которые будут на ЕГЭ, есть целая группа заданий, в которых дан многоугольник, построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки - один квадратный сантиметр.

Просмотр содержимого презентации

Георг Пик

Георг Александр Пик,

австрийский математик

(10.08.1859 - 13.07.1942)

Формула была открыта в 1899 г.

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах):
N – количество узлов внутри треугольника;

* Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)
N = 34 (обозначены синим)

Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)
N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)
N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)
N = 43 (обозначены синим)

Отметим узлы:

M = 11 (обозначены красным)
N = 5 (обозначены синим)

Решите самостоятельно:

1. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1 см. Ответ дайте в квадратных сантиметрах.

4. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1 см. Ответ дайте в квадратных сантиметрах .

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответы:

№ задания

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема . На первый взгляд, она может показаться сложной. Но достаточно решить пару задач - и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

Узел координатной стеки - это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

Обозначение:

На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n - число узлов внутри данного многоугольника, k - число узлов, которые лежат на его границе (граничных узлов).

В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно n = 10. На третей картинке отмечены узлы лежащие на границе, их всего k = 6.

Возможно, многим читателям непонятно, как считать числа n и k . Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника - замкнутая ломаная , которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются три линии :

Собственно, ломаная;
Горизонтальная линия координатной сетки;
Вертикальная линия.

Посмотрим, как все это работает в настоящих задачах.

Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: n = 1. Граничных узлов - целых шесть: три совпадают с вершинами треугольника , а еще три лежат на сторонах. Итого k = 6.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего n = 2. Граничных узлов: k = 7, из которых 4 являются вершинами четырехугольника , а еще 3 лежат на сторонах.

Остается подставить числа n и k в формулу площади:

Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Важное замечание по площадям

Но формула - это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю . Получим:

Числа n и k - это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью . Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью вида ***,5. Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Формула Пика

1. Введение

2. Формула Пика. Доказательство I .

Доказательство II .

Доказательство Ш.

3. Задачи.

4. Формула площади многоугольника через координаты вершин.

5. Задачи.

6. Литература

Формула Пика.

1. Введение.

В истории черпаем мы мудрость,

в поэзии - остроумие,

в математике - проницательность.

Ф. Бэкон

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.

Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причудливо? Оказывается, площади многоугольников, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

2. Формула Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Доказательство I .

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна
.

180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 ,

= В + – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + – 1 ,

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Г = 20 (синие точки).

Получаем, S =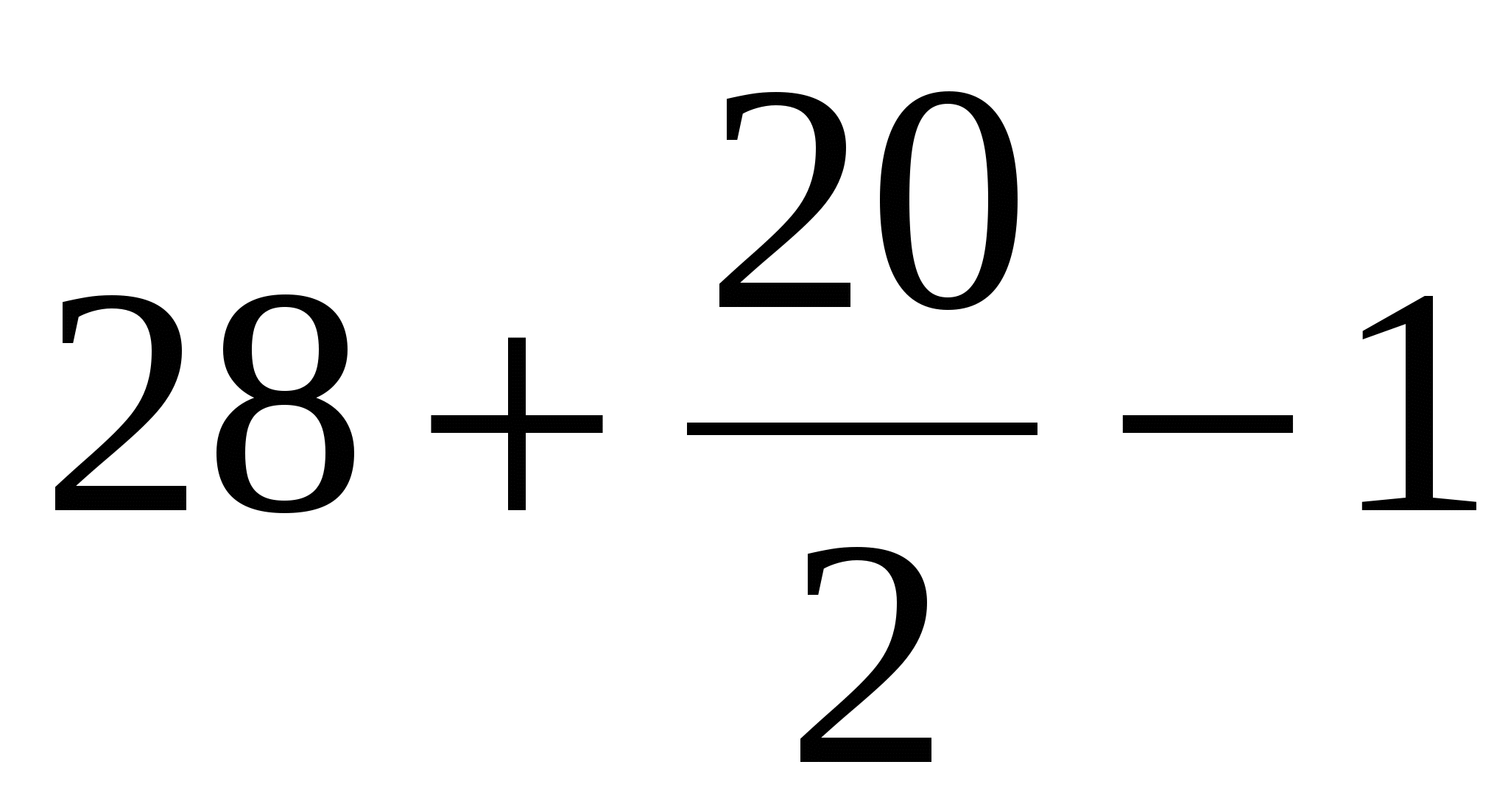
= 37 кв.ед.

Доказательство II .

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) =
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: =
для внутренней точки многоугольника, =
для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) =
+
= В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M 1 и M 2 с вершинами в узлах решетки. Тогда f (M) = f (M 1) + f (M 2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M 1 и M 2 , то она верна и для третьего.

Если M - прямоугольник со сторонами p и q , направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) +
= pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M 1 и M 2 и воспользовавшись тем, что f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Доказательство Ш.

Связь между площадью фигуры и количеством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.

Обозначим через В количество узлов, лежащих внутри прямоугольника, а через Г - количество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 граничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу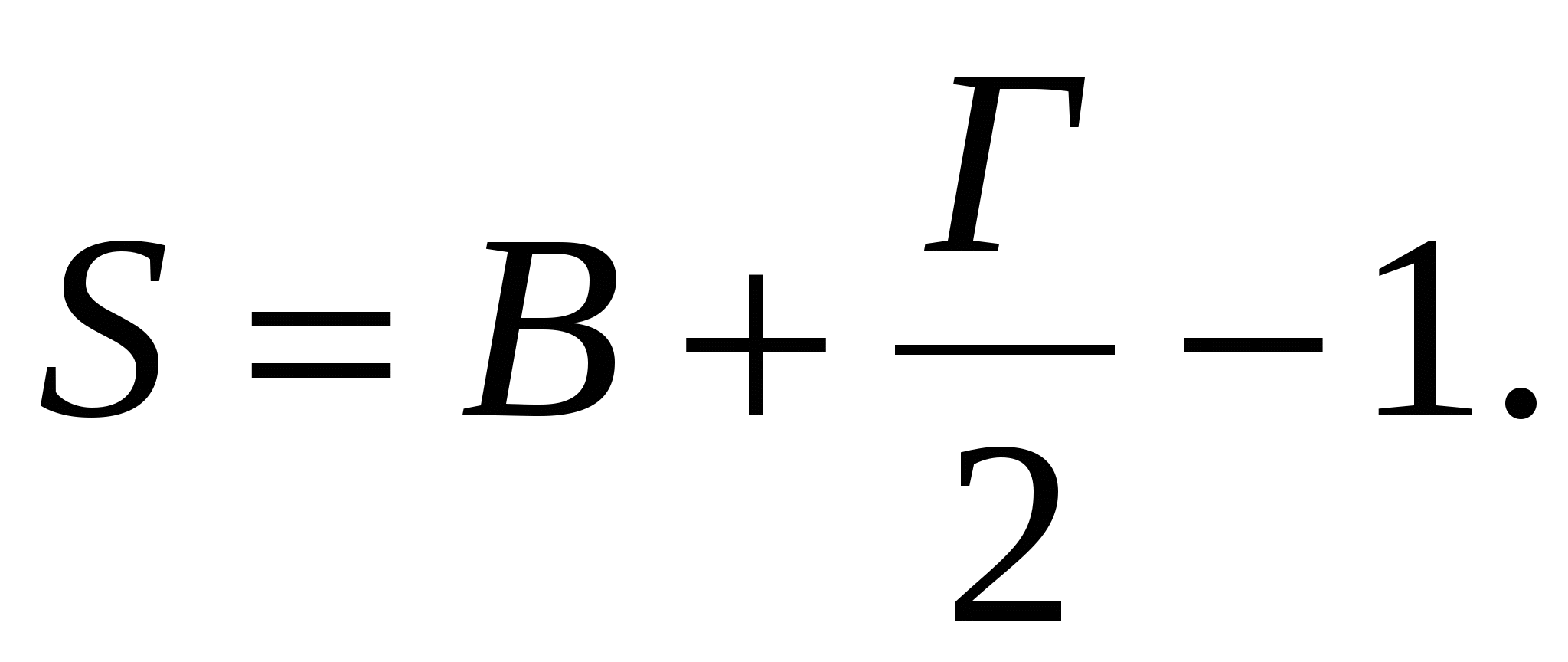

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S м площадь многоугольника М с вершинами в узлах, а через П м – величину
, где В м – число узлов внутри М, а Г м - число узлов на границе. Тогда формулу Пика можно записать в виде
.

Доказательство формулы разобьем на несколько шагов.

Шаг 1.

Если многоугольник М с вершинами в узлах сетки разрезан на 2 многоугольника М 1 и М 2 , также имеющих вершины только в узлах сетки, то
. Пусть многоугольник М разрезан на многоугольники М 1 и М 2 с вершинами в узлах отрезком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (например, С), то для многоугольника М он внутренний, а для многоугольников М 1 и М 2 – граничный. Поэтому его вклад в П м равен 1, а в каждое из выражений
и
– по 0,5, то есть вклады такого узла в П м и
равны.

Рассмотрим узлы А и В. Они граничные как для М , так и для М 1 , М 2 .

Поэтому вклад каждого из этих узлов в П м равен 0,5 а в
- единице. Значит, суммарный вклад узлов А и В в П м равен 1, что на 1 меньше, чем их вклад в
. Но
, а .

Из общего «вклада» всех узлов П м вычитается 1, а из
вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак,
.

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М 1 и М 2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М 1 , М 2 , то она верна и для третьего многоугольника.

Пусть, например, она верна для М 1 и М 2 , то есть
. Тогда (по первому шагу) , но (по первому шагу) последнее выражение равно П м , а равенство
и есть формула Пика.

Шаг 3.

Докажем формулу Пика для прямоугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Треугольник АВС достроим до прямоугольника ABCD .

Для прямоугольников формула Пика верна: S ABCD = П ABCD . Согласно первому шагу П ABCD = П ABC + П ACD , П ABC = П ACD , так что П ABCD = 2П ABC . Но S ABCD = 2 S ABC . Поэтому S ABC = П ABC .

Шаг 4.

Формула Пика верна для произвольного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямоугольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник можно разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

3. Задачи.

Найдите площади фигур:

1
.