Вычисление из под корня. Исследовательская работа на тему: "Извлечение квадратных корней из больших чисел без калькулятора"

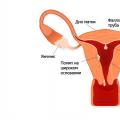
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.

Ниже мы по очереди рассмотрим основные способы извлечения корней.

Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.

Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.

Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.

Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.

Приступим.

Использование таблицы квадратов, таблицы кубов и т.д.

В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?

Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .

Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.

Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.

Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.

В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .

Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.

Разложение подкоренного числа на простые множители

Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.

Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .

Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.

Разберемся с этим при решении примеров.

Пример.

Извлеките квадратный корень из 144 .

Решение.

Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .

Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.

Разложим 144 на простые множители:

То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .

Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .

Ответ:

Для закрепления материала рассмотрим решения еще двух примеров.

Пример.

Вычислите значение корня .

Решение.

Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .

Ответ:

Пример.

Является ли значение корня целым числом?

Решение.

Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.

Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.

Ответ:

Нет.

Извлечение корней из дробных чисел

Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.

Разберем пример извлечения корня из дроби.

Пример.

Чему равен квадратный корень из обыкновенной дроби 25/169 .

Решение.

По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.

Ответ:

Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.

Пример.

Извлеките кубический корень из десятичной дроби 474,552 .

Решение.

Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .

Ответ:

Извлечение корня из отрицательного числа

Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.

Рассмотрим решение примера.

Пример.

Найдите значение корня .

Решение.

Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .

Приведем краткую запись решения: .

Ответ:

Порязрядное нахождение значения корня

В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.

На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.

Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =0<5 , 10 2 =100>5 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.

Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.

Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .

Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.

Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9 , вычисляя соответственно 0 2 , 1 2 , …, 9 2 до того момента, пока не получим значение, большее подкоренного числа 5 . Все эти вычисления удобно представлять в виде таблицы:

Так значение разряда единиц равно 2 (так как 2 2 <5 , а 2 3 >5 ). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9 , сравнивая полученные значения с подкоренным числом 5 :

Так как 2,2 2 <5 , а 2,3 2 >5 , то значение разряда десятых равно 2 . Можно переходить к нахождению значения разряда сотых:

Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .

Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.

Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151,186 , таким образом, старшим разрядом является разряд десятков.

Определим его значение.

Так как 10 3 <2 151,186 , а 20 3 >2 151,186 , то значение разряда десятков равно 1 . Переходим к единицам.

Таким образом, значение разряда единиц равно 2 . Переходим к десятым.

Так как даже 12,9 3 меньше подкоренного числа 2 151,186 , то значение разряда десятых равно 9 . Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.

На этом этапе найдено значение корня с точностью до сотых: .

В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.

Список литературы.

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 - 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.

Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:

Вычисляем:

Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.

Суть рассматриваемого нами метода - это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.

Извлечём корень из 190969.

Сначала определим — между какими числами (кратными ста) лежит наш результат.

Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как

400 2 =160000 и 500 2 =250000

Действительно:

посредине, ближе к 160 000 или к 250 000?

Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:

Действительно, он меньше 450, так как 190 969 < 202 500.

Теперь проверим число 440:

Значит наш результат меньше 440, так как 190 969 < 193 600.

Проверяем число 430:

Мы установили, что результат данного корня лежит в пределах от 430 до 440.

Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.

Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.

*Только они при возведении в квадрат могут дать 9 в конце.

Проверяем:

Значит результат корня будет равен 437.

То есть, мы как бы «нащупали» верный ответ.

Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.

Извлеките самостоятельно корень из 148996

Такой дискриминант получается в задаче:

Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.

Посмотреть решение

Результат корня находится между числами 300 и 400:

300 2 =90000 400 2 =160000

Действительно, 90000<148996<160000.

Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.

Вычислим разности 148996 - 90000=58996 и 160000 - 148996=11004.

Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.

Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

В математике вопрос о том, как извлекать корень, считается относительно несложным. Если возвести в квадрат числа из натурального ряда: 1, 2, 3, 4, 5 …n, то у нас получится следующий ряд квадратов: 1, 4, 9, 16 …n 2 . Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.

Корень из числа: правила вычисления и примеры

Итак, мы возвели число 2 в квадрат, то есть умножили его само на себя и получили 4. А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.

Степень корня – всегда натуральное число, то есть нельзя решить такое уравнение: корень в степени 3,6 из n.

Квадратный корень

Вернемся к вопросу о том, как извлечь корень квадратный из 4. Так как возводили мы число 2 именно в квадрат, то и корень будем извлекать квадратный. Для того чтобы правильно извлечь корень из 4, нужно просто правильно подобрать число, которое при возведении в квадрат дало бы число 4. И это, конечно же, 2. Посмотрите на пример:

2 2 =4
Корень из 4 = 2

Этот пример довольно простой. Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.

8 2 =64
Корень из 64=8

Кубический корень

Как выше было сказано, корни бывают не только квадратными, на примере попробуем более понятно объяснить, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:

3x3x3=27
Естественно, кубическим корнем из числа 27 будет тройка:
Корень 3 из 27 = 3

Допустим, необходимо найти кубический корень из 64. Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.

4 3 =64
Корень 3 из 64 = 4

Извлечь корень из числа на калькуляторе

Конечно, лучше всего учиться извлекать квадратные, кубические и корни другой степени на практике, путем решения многих примеров и запоминания таблицы квадратов и кубов небольших чисел. В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.

Не из каждого числа можно извлечь целый корень, рассмотрим следующий пример:

Корень из 1859 = 43,116122…

Вы можете параллельно попробовать решить этот пример на калькуляторе. Как видите, полученное число не является целым, более того, набор цифр после запятой является не конечным. Более точный результат могут дать специальные инженерные калькуляторы, на дисплее же обычных полный результат просто не умещается. А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.

Если вам необходимо извлечь корень третьей степени на простом калькуляторе, то необходимо нажать дважды на кнопку со знаком корня. Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:

Корень 3 из 1859 = 6,5662867…

То есть, если число 6,5662867… возвести в третью степень, то мы получим приблизительно 1859. Таким образом, извлекать корни из чисел не сложно, достаточно лишь запомнить выше приведенные алгоритмы.

Желательно инженерный – такой, в котором имеется кнопочка со знаком корня: «√». Обычно для извлечения корня достаточно набрать само число, а потом нажать на кнопку: «√».

В большинстве современных мобильных телефонов имеется приложение «калькулятор» с функцией извлечения корня. Порядок нахождения корня числа с помощью телефонного калькулятора аналогичен вышеизложенному.
Пример.
Найти из 2.
Включаем калькулятор (если он выключен) и последовательно нажимаем кнопки с изображением двойки и корня («2» «√»). Нажимать на клавишу «=», как правило, не нужно. В результате получаем число типа 1,4142 (количество знаков и «округленность» зависит от разрядности и настроек калькулятора).
Примечание: при попытке найти корень калькулятор обычно выдает об ошибке.

Если есть доступ к компьютеру, то найти корень числа очень просто.
1. Можно воспользоваться приложением «Калькулятор», имеющемся практически на любом компьютере. Для Windows ХР эту программу можно запустить следующим образом:
«Пуск» - «Все программы» - «Стандартные» - «Калькулятор».
Вид лучше установить «обычный». Кстати, в отличие от реального калькулятора кнопка для извлечения корня помечена как «sqrt», а не «√».

Если добраться до калькулятора указанным способом не , то можно запустить стандартный калькулятор «вручную»:
«Пуск» - «Выполнить» - «calc».
2. Для нахождения корня числа можно также воспользоваться некоторыми программами, установленными на компьютере. Кроме того, программы собственный встроенный калькулятор.

Например, для приложения MS Excel можно проделать следующую последовательность действий:
Запускаем MS Excel.

Записываем в любую клетку число, из которого нужно извлечь корень.

Помещаем указатель клетки на другое место

Нажимаем кнопочку выбора функции (fx)

Выбираем функцию «КОРЕНЬ»

В качестве аргумента функции указываем клетку с числом

Нажимаем «ОК» или «Еnter»
Преимуществом данного способа является то, что теперь достаточно ввести в клетку с числом любое значение, как в с функцией тут же появляется .
Примечание.
Имеется несколько других, более экзотических способа найти корень числа. Например, «уголком», с помощью логарифмической линейки или таблиц Брадиса. Однако, в этой статье эти методы не рассматриваются ввиду их сложности и практической бесполезности.

Видео по теме

Источники:

как находить корень числа

Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни квадратные и корни большей степени из числа. Корень степени "n" из числа "a" представляет собой число, n-я степень которого и есть число "a".

Инструкция

Чтобы найти корень "n" из , сделайте следующее.

Нажмите на своем компьютере «Пуск» - «Все программы» - «Стандартные». Затем войдите в подраздел «Служебные» и выберите «Калькулятор». Можете сделать это вручную: нажмите «Пуск», введите «calk» в строку «выполнить» и нажмите «Enter». Откроется . Для извлечения корня квадратного из какого-либо числа, введите это в строку калькулятора и нажмите кнопку с надписью «sqrt». Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным.

Для того чтобы извлечь корень, степень которого выше второй, нужно воспользоваться другим видом калькулятора. Для этого в интерфейсе калькулятора нажмите кнопку «Вид» и в меню выберите строку «Инженерный» или «Научный». Этот вид калькулятора имеет необходимую для вычисления корня n-й степени функцию.

Для извлечения корня третьей степени (), на «инженерном» калькуляторе наберите нужное число и нажмите кнопку «3√». Для получения корня, степень которого выше 3-й, наберите нужное число, нажмите кнопку со значком «y√x» и затем введите число – показатель степени. После этого нажмите знак равенства (кнопка «=») и вы получите искомый корень.

Если на вашем калькуляторе отсутствует функция «y√x», следующее.

Для извлечения кубического корня введите подкоренное выражение, потом поставьте в чек боксе, который расположен рядом с надписью «Inv», отметку. Этим действием вы переведете функции кнопок калькулятора на обратные, т.е., щелкнув по кнопке для возведения в куб, вы произведете извлечение корня кубического. На кнопке, которая вам

Соколов Лев Владимирович, учащийся 8 класса МКОУ «Тугулымская В(С)ОШ»

Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.

Скачать:

Предварительный просмотр:

Районная научно-практическая конференция

обучающихся Тугулымского городского округа

Извлечение квадратных корней из больших чисел без калькулятора

Исполнитель: Лев Соколов,

МКОУ «Тугулымская В(С)ОШ»,

8 класс

Руководитель: Сидорова Татьяна

Николаевна

р.п. Тугулым, 2016 г.

Введение 3

Глава 1. Способ разложения на простые множители 4

Глава 2. Извлечение квадратного корня уголком 4

Глава 3. Способ использования таблицы квадратов двузначных чисел 6

Глава 4. Формула Древнего Вавилона 6

Глава 6. Канадский метод 7

Глава 7. Метод подбора угадыванием 8

Глава 8 . Метод вычетов нечётного числа 8

Заключение 10

Список литературы 11

Приложение 12

Введение

Актуальность исследования, когда я изучал тему квадратные корни в этом учебном году, то меня заинтересовал вопрос, как можно извлечь квадратный корень из больших чисел без калькулятора.

Я заинтересовался и решил изучить этот вопрос глубже, чем он изложен в школьной программе, а также приготовить мини-книжечку с наиболее простыми способами извлечения квадратных корней из больших чисел без калькулятора.

Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.

Задачи:

Изучить литературу по данному вопросу.
Рассмотреть особенности каждого найденного способа и его алгоритм.
Показать практическое применение полученных знаний и оценить

Степень сложности в использовании различных способов и алгоритмов.

Создать мини-книжечку по самым интересным алгоритмам.

Объект исследования: математические символы – квадратные корни.

Предмет исследования: особенности способов извлечения квадратных корней без калькулятора.

Методы исследования:

Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
Сравнение найденных способов.
Анализ полученных способов.

Все знают, что извлечь квадратный корень без калькулятора - это очень сложная

задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Например, таблица квадратов целых чисел не даёт ответ на такие вопросы, как, например, извлечь корень из 75, 37,885,108,18061 и другие даже приблизительно.

Также часто на экзаменах ОГЭ и ЕГЭ пользование калькулятором запрещено и нет

таблицы квадратов целых чисел, а надо извлечь корень из 3136 или 7056 и т.д.

Но изучая литературу по данной теме, я узнал, что извлекать корни из таких чисел

возможно и без таблицы и калькулятора, люди научились задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.

Глава 1. Способ разложения на простые множители

Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.

Таким способом принято пользоваться при решении заданий с корнями в школе.

3136│2 7056│2

1568│2 3528│2

784│2 1764│2

392│2 882│2

196│2 441│3

98│2 147│3

49│7 49│7

7│7 7│7

√3136 = √2²∙2²∙2²∙7² = 2∙2∙2∙7 = 56 √3136 = √2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84

Многие применяют его успешно и считают единственным. Извлечение корня разложением на множители - трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 209764? Разложение на простые множители дает произведение 2∙2∙52441. А как быть дальше? С этой задачей сталкиваются все, и спокойно в ответе записывают остаток от разложения под знак корня. Методом проб и ошибок, подбором разложение, конечно, можно сделать, если быть уверенным в том, что получится красивый ответ, но практика показывает, что очень редко предлагаются задания с полным разложением. Чаще мы видим, что корень до конца не извлечь.

Поэтому, этот способ лишь частично решает проблему извлечения без калькулятора.

Глава 2. Извлечение квадратного корня уголком

Для извлечения квадратного корня уголком и рассмотрим алгоритм:
1-й шаг. Число 8649 разбиваем на грани справа налево; каждая из которых должна содержать две цифры. Получаем две грани: .
2-й шаг. Извлекаем квадратный корень из первой грани 86, получаем с недостатком. Цифра 9 –это первая цифра корня.
3-й шаг. Число 9 возводим в квадрат (9 2 = 81) и число 81 вычитаем из первой грани, получаем 86- 81=5. Число 5 – первый остаток.
4-й шаг. К остатку 5 приписываем вторую грань 49, получаем число 549.

5-й шаг . Удваиваем первую цифру корня 9 и, записывая слева, получаем-18

К числу нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Это цифра 3. Она находится путем подбора: количество десятков числа 549, то есть число 54 делится на 18, получаем 3, так как 183 ∙ 3 = 549. Цифра 3 – это вторая цифра корня.

6-й шаг. Находим остаток 549 – 549 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 93.

Пприведу еще пример: извлечь √212521

Шаги алгоритма	Пример	Комментарии
Разбить число на группы по 2 цифры в каждой справа налево	21’ 25’ 21	Общее число образовавшихся групп определяет количество цифр в ответе
Для первой группы цифр подобрать цифру, квадрат которой будет наибольшим, но не превосходящим числа первой группы	1 группа – 21 4 2 =16 цифра - 4	Найденная цифра записывается в ответе на первом месте
Из первой группы цифр вычесть найденный на шаге 2 квадрат первой цифры ответа	21’ 25’ 21
К остатку, найденному на шаге 3, приписать справа (снести) вторую группу цифр	21’ 25’ 21 16__
К удвоенной первой цифре ответа приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходила числа, найденного на шаге 4	42=8 цифра – 6 866=516	Найденная цифра записывается в ответе на втором месте
Из числа, полученного на шаге 4 вычесть число, полученное на шаге 5. Снести к остатку третью группу	21’ 25’ 21
К удвоенному числу, состоящему из первых двух цифр ответа, приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру был наибольшим, но не превосходило числа, полученного на шаге 6	462=92 цифра 1 9211=921	Найденная цифра записывается в ответе на третьем месте
Записать ответ	√212521=461

Глава 3. Способ использования таблицы квадратов двузначных чисел

Про этот способ я узнал из Интернета. Способ очень простой и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых без калькулятора. Одно условие для этого метода – наличие таблицы квадратов чисел до 99.

(Она есть во всех учебниках алгебры 8 класса, и на экзамене ОГЭ предлагается в качестве справочного материала.)

Откройте таблицу и проверьте скорость нахождения ответа. Но сначала несколько рекомендаций: самый левый столбик – это будут в ответе целые, самая верхняя строчка – это десятые в ответе. А дальше всё просто: закройте две последние цифры числа в таблице и найдите нужное вам, не превосходящее подкоренное число, и далее действуйте по правилам этой таблицы.

Рассмотрим на примере. Найдём значение √87.

Закрываем две последние цифры у всех чисел в таблице и находим близкие для 87 – таких только два 86 49 и 88 37. Но 88 – это уже много.

Значит, остаётся только одно – 8649.

Левый столбик даёт ответ 9 (это целых), а верхняя строчка 3 (это десятых). Значит √87≈ 9,3. Проверим на МК √87 ≈ 9,327379.

Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.

Глава 4. Формула Древнего Вавилона

Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b, где а 2 ближайший к числу х точный квадрат натурального числа а (а 2 . (1)

Извлечем с помощью формулы (1) корень квадратный, например из числа 28:

Результат извлечения корня из 28 с помощью МК 5,2915026.

Как видим способ вавилонян дает хорошее приближение к точному значению корня.

Глава 5. Способ отбрасывания полного квадрата

(только у четырехзначных чисел)

Сразу стоит уточнить, что этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.

Извлечение корней до числа 75 2 = 5625

Например: √¯3844 = √¯ 37 00 + 144 = 37 + 25 = 62.

Число 3844 представим в виде суммы, выделив из этого числа квадрат 144, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (37) прибавляем всегда 25 . Получим ответ 62.

Так можно извлекать только квадратные корни до числа 75 2 =5625!

2) Извлечение корней после числа 75 2 = 5625

Как же устно извлечь квадратные корни из чисел больше 75 2 =5625?

Например: √7225 = √ 70 00 + 225 = 70 + √225 = 70 + 15 = 85.

Поясним,7225 представим в виде суммы 7000 и выделенного квадрата 225. Затем к числу сотен прибавить квадратный корень из 225, равный 15.

Получим ответ 85.

Этот способ нахождения очень интересен и в какой – то мере оригинален, но в ходе моего исследования встретился только один раз в работе пермского преподавател.

Возможно, он мало изучен или имеет какие – то исключения.

Он достаточно сложен в запоминании из – за двойственности алгоритма и применим только для четырёхзначных чисел точных корней, но я проработал множество примеров и убедился в его правильности. Кроме всего этот способ доступен тем, кто уже запомнил наизусть квадраты чисел от 11 до 29, ведь без их знания он будет бесполезен.

Глава 6. Канадский метод

√ X = √ S + (X - S) / (2 √ S), гдеX - число, из которого необходимо извлечь квадратный корень, а S - число ближайшего точного квадрата.

Давайте попробуем извлечь квадратный корень из 75

√ 75 = 9 + (- 6/18) = 9 - 0,333 = 8,667

При детальном изучении этого метода легко можно доказать его сходство с вавилонским и поспорить за авторские права изобретения этой формулы, если такие есть в действительности. Метод несложный и удобный.

Глава 7. Метод подбора угадыванием

Этот метод предлагают английские студенты математического колледжа Лондона, но каждый в своей жизни хоть раз непроизвольно пользовался этим методом. Он основан на подборе разных значений квадратов близких чисел путём сужения области поиска. Овладеть этим способом может каждый, но вот пользоваться вряд ли, потому что он требует многократного вычисления произведения столбиком не всегда правильно угаданных чисел. Этот способ проигрывает и в красоте решения, и по времени. Алгоритм прост:

Предположим, вы хотите извлечь квадратный корень из 75.

Так как 8 2 = 64 и 9 2 = 81, вы знаете, ответ находится где-то между ними.

Попробуйте возвести 8,5 2 и вы получите 72,25 (слишком мало)

Теперь попробуйте 8,6 2 и вы получите 73,96 (слишком небольшой, но все ближе)

Теперь попробуйте 8,7 2 и вы получите 75,69 (слишком большая)

Теперь вы знаете, ответ находится между 8,6 и 8,7

Попробуйте возвести 8,65 2 и вы получите 74,8225 (слишком мало)

Теперь попробуйте 8,66 2 ... и так далее.

Продолжайте, пока не получите ответ достаточно точный для вас.

Глава 8. Метод вычетов нечётного числа

Многие знают метод извлечения квадратного корня разложением числа на простые множители. В своей работе представлю ещё один способ, с помощью которого можно узнать целую часть квадратного корня числа. Способ очень простой. Заметим, что для квадратов чисел верны следующие равенства:

1=1 2

1+3=2 2

1+3+5=3 2

1+3+5+7=4 2 и т.д.

Правило: узнать целую часть квадратного корня числа можно вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и сочтя количество выполненных действий.

Например, чтобы получить квадратный корень из 36 и 121 это:

Общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6.

Общее количество вычитаний = 11, поэтому √121 = 11.

Еще пример: найдём √529

Решение: 1)_529

2)_528

3)_525

4)_520

5)_513

6)_504

7)_493

8)_480

9)_465

10)_448

11)_429

12)_408

13)_385

14)_360

15)_333

16)_304

17)_273

18)_240

19)_205

20)_168

21)_129

22)_88

23)_45

Ответ: √529 = 23

Ученые называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня. Попробуйте извлечь квадратный корень из числа, например, 5963364 этим способом и вы поймёте, что он «работает», безусловно, без погрешностей для точных корней, но очень - очень длинный в решёнии.

Заключение

Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от калькулятора.

В результате проведённого исследования я пришел к выводу: различные способы извлечения квадратного корня без калькулятора необходимы в школьном курсе математики, чтобы развивать навыки вычислений.

Теоретическая значимость исследования – систематизированы основные методы извлечения квадратных корней.

Практическая значимость: в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами (Приложение1).

Литература и сайты Интернета:

И.Н. Сергеев, С.Н. Олехник, С.Б.Гашков «Примени математику». – М.: Наука, 1990
Керимов З., «Как найти целый корень?» Научно-популярный физико-математический журнал "Квант" №2, 1980
Петраков И.С. «математические кружки в 8-10 классах»; Книга для учителя.

–М.:Просвещение,1987

Тихонов А.Н., Костомаров Д.П. «Рассказы о прикладной математики».- М.: Наука. Главная редакция физико- математической литературы, 1979
Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
Жохов В.И., Погодин В.Н. Справочные таблицы по математике.-М.: ООО «Издательство «РОСМЭН-ПРЕСС», 2004.-120 с.
http://translate.google.ru/translate
http://www.murderousmaths.co.uk/books/sqroot.htm
http://ru.wikipedia.ord /wiki /teorema/

Добрый день, уважаемые гости!

Меня зовут Лев Соколов, я учусь в 8 классе в вечерней школе.

Представляю вашему вниманию работу на тему: « Извлечение квадратных корней из больших чисел без калькулятора».

При изучении темы квадратные корни в этом учебном году, меня заинтересовал вопрос, как можно извлечь квадратный корень из больших чисел без калькулятора и я решил изучить его глубже, так как на следующий год мне предстоит сдавать экзамен по математике.

Цель моей работы: найти и показать способы извлечения квадратных корней без калькулятора

Для достижения цели я решал следующие задачи:

1. Изучить литературу по данному вопросу.

2. Рассмотреть особенности каждого найденного способа и его алгоритм.

3. Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов.

4.Создать мини-книжечку по самым интересным алгоритмам.

Объектом моего исследования стали квадратные корни.

Предмет исследования: способы извлечения квадратных корней без калькулятора.

Методы исследования:

1. Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.

2. Сравнение и анализ найденных способов.

Я нашел и изучил 8 способов извлечения квадратных корней без калькулятора и отработал их на практике. Название найденных способов приведены на слайде.

Я остановлюсь на тех из них, которые мне понравились.

Покажу на примере, как можно способом разложения на простые множители извлечь квадратный корень из числа 3025.

Основной недостаток этого способа - он занимает много времени.

С помощью формулы Древнего Вавилона я извлеку квадратный корень из этого же числа 3025.

Способ удобен только для малых чисел.

Из этого же числа 3025 извлекаем квадратный корень уголком.

На мой взгляд, это самый универсальный способ, он применим к любым числам.

В современной науке известно много способов извлечения квадратного корня без калькулятора, но я изучил не все.

Практическая значимость моей работы: в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами.

Результаты моей работы могут успешно применяться на уроках математики, физики и других предметах, где требуется извлечение корней без калькулятора.

Спасибо за внимание!

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Извлечение квадратных корней из больших чисел без калькулятора Исполнитель: Лев Соколов, МКОУ « Тугулымская В(С)ОШ»,8 класс Руководитель: Сидорова Татьяна Николаевна I категория, учитель математики р.п. Тугулым

Правильному применению методов можно научиться, применяя и на разнообразных примерах. Г. Цейтен Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора. Задачи: - Изучить литературу по данному вопросу. - Рассмотреть особенности каждого найденного способа и его алгоритм. - Показать практическое применение полученных знаний и оценить степень сложности в использовании различных способов и алгоритмов. - Создать мини-книжечку по самым интересным алгоритмам.

Объект исследования: квадратные корни Предмет исследования: способы извлечения квадратных корней без калькулятора. Методы исследования: Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора. Сравнение найденных способов. Анализ полученных способов.

Способы извлечения квадратного корня: 1. Способ разложения на простые множители 2. Извлечение квадратного корня уголком 3. Способ использования таблицы квадратов двузначных чисел 4. Формула Древнего Вавилона 5. Способ отбрасывания полного квадрата 6. Канадский метод 7. Метод подбора угадыванием 8. Метод вычетов нечётного числа

Способ разложения на простые множители Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения. 3136│2 7056│2 209764│2 1568│2 3528│2 104882│2 784│2 1764│2 52441│229 392│2 882│2 229│229 196│2 441│3 98│2 147│3 √209764 = √2∙2∙52441 = 49│7 49│7 = √2²∙229² = 458. 7│7 7│7 √3136 = √ 2²∙2²∙2²∙7² = 2∙2∙2∙7 = 56. √7056 = √2²∙2²∙3²∙7² = 2∙2∙3∙7 = 84. Не всегда легко можно разложить, чаще до конца не извлекается, занимает много времени.

Формула Древнего Вавилона (Вавилонский метод) Алгоритм извлечения квадратного корня древневавилонским способом. 1 . Представить число с в виде суммы а ² + b , где а ² ближайший к числу с точный квадрат натурального числа а (а ² ≈ с); 2. Приближенное значение корня вычисляется по формуле: Результат извлечения корня с помощью калькулятора равен 5,292.

Извлечение квадратного корня уголком Способ почти универсальный, так как применим к любым числам, но составление ребуса (угадывание цифры на конце числа) требует логики и хороших вычислительных навыков столбиком.

Алгоритм извлечения квадратного корня уголком 1. Разбиваем число (5963364) на пары справа налево (5`96`33`64) 2. Извлекаем квадратный корень из первой слева группы (- число 2). Так мы получаем первую цифру числа. 3. Находим квадрат первой цифры (2 2 =4). 4. Находим разность первой группы и квадрата первой цифры (5-4=1). 5.Сносим следующие две цифры (получили число 196). 6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4). 7.Теперь необходимо найти вторую цифру числа: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 - вторая цифра числа &. 8. Находим разность (196-176=20). 9. Сносим следующую группу (получаем число 2033). 10. Удваиваем число 24, получаем 48. 11. 48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа. Далее процесс повторяется.

Метод вычетов нечётного числа (арифметический способ) Алгоритм извлечения квадратного корня: Вычитать нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитать количество выполненных действий – это число есть целаячасть числа извлекаемого квадратного корня. Пример 1: вычислить 1. 9 − 1 = 8; 8 − 3 = 5; 5 − 5 = 0. 2. Выполнено 3 действия

36 - 1 = 35 - 3 = 32 - 5 = 27 - 7 = 20 - 9 = 11 - 11 = 0 общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6. 121 – 1 = 120 - 3 = 117- 5 = 112 - 7 = 105 - 9 = 96 - 11 = 85 – 13 = 72 - 15 = 57 – 17 = 40 - 19 = 21 - 21 = 0 Общее количество вычитаний = 11, поэтому квадратный корень из 121 = 11. 5963364 = ??? Российские учёные «за глаза» называют его «методом черепахи» из-за его медлительности. Он неудобен для больших чисел.

Теоретическая значимость исследования – систематизированы основные методы извлечения квадратных корней. Практическая значимость: в создании мини-книжечки, содержащей опорную схему извлечения квадратных корней различными способами.

Спасибо за внимание!

Предварительный просмотр:

При решении некоторых задач потребуется извлечь квадратный корень из крупного числа. Как это сделать?

Метод вычетов нечётного числа.

Способ очень простой. Заметим, что для квадратов чисел верны следующие равенства:

1=1 2

1+3=2 2

1+3+5=3 2

1+3+5+7=4 2 и т.д.

Например, чтобы получить квадратный корень из 36 и 121 это:

36 - 1 = 35 - 3 = 32 - 5 = 27 - 7 = 20 - 9 = 11 - 11 = 0

Общее количество вычитаний = 6, поэтому квадратный корень из 36 = 6.

121 - 1 = 120 - 3 = 117- 5 = 112 - 7 = 105 - 9 = 96 - 11 = 85 – 13 = 72 - 15 = 57 – 17 = 40 - 19 = 21 - 21 = 0

Общее количество вычитаний = 11, поэтому √121 = 11.

Канадский метод.

Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула:

√ X = √ S + (X - S) / (2 √ S), где X - число, из которого необходимо извлечь квадратный корень, а S - число ближайшего точного квадрата.

Пример. Извлечь квадратный корень из 75.

X = 75, S = 81. Это означает, что √ S = 9.

Просчитаем по этой формуле √75: √ 75 = 9 + (75 - 81) / (2∙ 9)
√ 75 = 9 + (- 6/18) = 9 - 0,333 = 8,667

Способ извлечения квадратного корня уголком.

1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)

2. Извлекаем квадратный корень из первой слева группы ( - число 2). Так мы получаем первую цифру числа.

3. Находим квадрат первой цифры (2 2 =4).

4. Находим разность первой группы и квадрата первой цифры (5-4=1).

5.Сносим следующие две цифры (получили число 196).

6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).

7.Теперь необходимо найти вторую цифру числа: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 - вторая цифра числа &.

8. Находим разность (196-176=20).

9. Сносим следующую группу (получаем число 2033).

10. Удваиваем число 24, получаем 48.

11.48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа.

Действие извлечения корня квадратного обратно действию возведения в квадрат.

√81= 9 9 2 =81.

Метод подбора.

Пример: Извлечь корень из числа 676 .

Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20

Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.

Осталось проверить: 24 2 = 576, 26 2 = 676.

Ответ: √ 676 = 26.

Еще пример: √6889 .

Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.

Проверяем: 83 2 = 6889.

Ответ: √6889 = 83 .

Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.

Например, найти √893025 .

Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.

Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.

Вавилонский метод.

Шаг №1. Представить число х в виде суммы: х=а 2 + b, где а 2 ближайший к числу х точный квадрат натурального числа а.

Шаг №2. Использовать формулу:

Пример. Вычислить .

Арифметический метод.

Вычитаем из числа все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю. Подсчитав количество выполненных действий, определяем, целую часть квадратного корня из числа.

Пример. Вычислить целую часть числа .

Решение. 12 - 1 = 11; 11 - 3 = 8; 8 - 5 = 3; 3 3 - целая часть числа . Итак, .

Метод (известный как метод Ньютона) заключается в следующем.

Пусть а 1 - первое приближение числа (в качестве а 1 можно брать значения квадратного корня из натурального числа - точного квадрата, не превосходящего .

Указанный способ позволяет извлекать квадратный корень из большого числа с любой точностью, правда с существенным недостатком: громоздкость вычислений.

Метод оценки.

Шаг №1. Выяснить диапазон, в котором лежит исходный корень (100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000).

Шаг №2 . По последней цифре определить на какую цифру заканчивается искомое число.

Цифра единиц числа х
Цифра единиц числа х 2

Шаг №3. Возвести в квадрат предполагаемые числа и определить из них искомое число.

Пример 1. Вычислить .

Решение. 2500 50 2 2 50

= *2 или = *8.

52 2 = (50 +2) 2 = 2500 + 2 · 50 · 2 + 4 = 2704;
58 2 = (60 − 2) 2 = 3600 − 2 · 60 · 2 + 4 = 3364.

Следовательно, = 58.