Проиллюстрируем поиск эффективных методов решения на некоторых фактах из школьной практики.
В одном из четвертых классов был предложен для решения следующий пример: 3 x 2 x 7 x 2 x 5 x 5; при этом учеников предупредили, что необходимо найти наиболее быстрый путь решения.
Ученики использовали шесть различных путей группировки чисел (5 x 5 = 25, 25 x 2 = 50, 50 x 2 = 100, 100 x 3 = 300, 300 x 7 = 2100 и др.), но наиболее рационального все же не нашли. Тогда учительница показала наиболее рациональную группировку: (2 x 5) x (2 x 5) = 100; 3 x 7 = 21; 21 x 100 = 2100.
Так формировалась у школьников при решении примеров привычка искать наиболее рациональные пути решения.
Такую привычку нужно вырабатывать у школьников на разном учебном материале планомерно и систематически, учитывая, что сама она не сформируется. Больше того, у младших школьников довольно часто проявляется обратная тенденция — идти по линии наименьшего сопротивления, не задумываясь давать первый, пришедший в голову ответ, использовать только наиболее привычный путь.
Такая тенденция ярко проявилась в следующем факте: ученикам двух четвертых классов был предложен пример с именованными числами. «Делимое — 1 сутки, делитель — 60 минут, найти частное».
Оказалось, что все ученики, кроме одного, решили этот пример так: раздробили 1 сутки в часы, затем раздробили 24 часа в минуты и, получив 1440 минут, разделили их на 60 (минут). Рациональный путь в решении примера , использованный только одним учеником, заключался в следующем: он раздробил сутки в часы, а данные 60 минут превратил также в часы, это дало ему возможность избежать громоздких вычислений, ответ был им получен делением 24 часов на 1 час. Этот ученик сумел преодолеть тенденцию повторять одну и ту же операцию раздробления и применил две противоположные операции.
Большую пользу для формирования привычки выбирать наиболее рациональный путь приносит решение арифметических задач. И не всегда для этой цели нужно использовать особо трудные «замысловатые» задачи, можно и на несложных задачах приучить детей размышлять над условием, анализировать его, тем самым освобождать многих детей от вредной привычки считать в задаче самым главным вычисления и спешить поэтому с получением числового ответа.
Так, ценное упражнение этого типа представляет задача: «В двух ящиках было 60 кг винограда; из одного ящика переложили в другой 16 кг. Сколько килограммов винограда стало в обоих ящиках?» Смысл подобных задач в том, чтобы приучить учеников воздерживаться от поспешного числового решения.
Как показало одно из исследований, многие школьники III и IV классов успешно справлялись с этой задачей. После внимательного ознакомления с условием они, не производя никаких вычислений, говорили: «Так и будет 60 кг», «Не изменится».
Однако немало школьников становились на неразумный путь, они производили вычисления (60—16 = 44, 44 + 16 = 60), даже не замечая того, что получили в результате те же исходные 60 кг.
Итак, воспитание у школьников в процессе обучения творческих поисков, формирование у них привычки размышлять — задача, без решения которой нельзя научить детей эффективным приемам самостоятельной работы.
Далее, необходимо у детей формировать шаг за шагом специальные умения, следя за тем, чтобы они научились правильно организовывать свою деятельность, умели бы направлять свои психические процессы: восприятие, память, мышление.
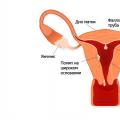
Очень важно научить детей подчинять свое восприятие поставленной задаче. Так, например, если в учебнике к арифметической задаче даны рисунок или схема, ученик должен уметь использовать их по назначению и видеть в них то, что может помочь ему решить данную задачу: в одних случаях увидеть в рисунке иллюстрацию, которая поясняет, о каких предметах идет речь в задаче, в других же — направить восприятие к иной цели, а именно на то, чтобы обнаружить в схеме те основные соотношения, которые даны в условии. Подход к этим двум видам графики должен быть у школьников различен: в одним случае они рассматривают иллюстрацию на первом этапе ознакомления с условием задачи, а в ходе ее решения уже не обращают на нее никакого внимания, во втором, наоборот, они ее используют в процессе самого решения.
Такое умение избирательно воспринимать иллюстрации вполне возможно сформировать у младших школьников.
Аналогично этому ученики должны уметь правильно использовать свою память. Широко распространен взгляд, что у детей младшего школьного возраста память механическая преобладает над памятью логической, смысловой, то есть дети запоминают, не стремясь осмыслить материал, установить между описываемыми фактами связь, выделить наиболее существенное и т. п.
Этот взгляд, как показывают работы многих психологов, не совсем верен. Преобладание механической памяти действительно имеется, но только при определенных условиях: если учителя начальных классов не работают над формированием у детей рациональных приемов запоминания. Но если такая работа ведется, младших школьников можно приучить осмысливать запоминаемый материал, в частности, приучить их обращать внимание в учебнике на те правила и определения, которые выделены жирным шрифтом, научить их (и это очень важно) контролировать себя при подготовке к уроку, для чего воспроизводить, то есть говорить себе самому (после прочтения в учебнике), то правило или то определение, которое нужно усвоить, приучить их к тому, чтобы не ограничиваться примерами, приведенными в учебнике, а обязательно придумывать свои и т. п.
Основная цель при формировании мышления — научить школьников самостоятельно решать относительно новые задачи , то есть такие, которые требуют активных поисков путей решения.
Существуют определенные правила, способствующие успеху этих поисков. Нетрудно заметить, что этими правилами прежде всего предусматривается выработка у школьников, приемов полного целенаправленного анализа.
Теперь возникает главный вопрос: какими путями школьники могут овладеть приемами рационального мышления?
Овладение этими приемами означает знание учеником того, как надо действовать, а это знание предполагает знание правила, в соответствии с которым применяется тот или иной способ. Совершенно ясно, однако, что учитель ничего не смог бы достичь, если бы он сообщал детям только готовые правила.
Сначала дети должны действовать в соответствии с этими правилами в процессе самостоятельного решения ими задач.
При этом учитель использует опыт детей в решении ими задач для того, чтобы раскрыть перед ними значение того или иного приема. Начать это делать необходимо уже с первого года обучения. Сначала учитель, а затем и сами дети формулируют значение используемого ими приема и контролируют его применение.
Это можно проиллюстрировать на примере, как первоклассники овладевают приемами правильного чтения текста задачи. Учитель вначале обращает внимание детей на важность умения прочитать текст задачи для ее успешного решения, указывает им на конкретные случаи, когда ошибки при чтении текста порождали трудности в решении задачи. Затем дети сами следят, как читают текст их товарищи по классу, и делают необходимые критические замечания: «слово «на» плохо прочла», «слово «меньше» не выделила», «плохо выделила числа» и т. п.
В этом случае не только формируются приемы анализа задачи, но также вырабатывается привычка контролировать себя и других, а это последнее является необходимой составной частью всякого умения.
Рациональный способ принятия решений в общей форме можно представить следующим образом.
Использование административного способа принятия решения выражается в том, что руководитель исследует альтернативы до тех пор, пока не обнаруживает удовлетворительного решения, т. е. обеспечивающего достижение цели на минимальном уровне. Он выбирает первую альтернативу, которая отвечает поставленным целям. Этот выбор ограничен ценностями, опытом и уровнем подготовки руководителя. Если у руководителя нет альтернатив, которые удовлетворяют минимальному уровню поставленных целей, он снижает значение этого уровня и принимает первую альтернативу. Он руководствуется только конкретными обстоятельствами ситуации и своими полномочиями.
При интуитивном способе принятия решения отсутствует систематический подход к выбору альтернатив. Этот способ часто используется творческими личностями. Исследования показывают, что характеристики этих индивидуумов включают большую потребность в независимости, деловой эгоизм, эрудицию, широкие интересы. Это не значит, что только такие руководители являются творческими личностями. Ими могут быть и те, кто использует другие способы принятия решений. Интуитивная форма встречается, когда решение принимается по случаю. Большинство же решений обосновывается с использованием сочетания рационального и интуитивного способов.
Кто должен принимать решение: индивидуум или группа? Существует несколько возможных схем: 1) руководитель может принимать решение один; 2) решение может быть принято руководителем после консультации с другими; 3) те, на кого влияет решение, могут принимать его как группа (руководитель при этом выступает как один из членов группы). Во всех случаях важно соблюдать установленные процедуры, выполнение которых обеспечивает необходимую обоснованность и надежность того или иного решения (табл. 16.4).
При групповом принятии решения обеспечивается участие тех, кого решение касается, и повышается их готовность осознанно выполнять решение. Облегчается координация последующей работы, улучшаются коммуникации, увеличивается разнообразие рассматриваемых альтернатив, расширяется объем используемой информации. Вместе с тем в литературе по управлению отмечаются и возможные недостатки группового принятия решений: оно может быть более длительным, группы могут оказаться менее решительными и чаще идут на компромисс, нередко попадают под чье-то влияние, отдельные индивидуумы могут использовать группу для усиления своего влияния;
иногда группы вообще не могут принять решение из-за внутренних конфликтов и несогласия.
Группы лучше всего использовать для принятия решений, когда особенно важна точность. Оперативность важнее в одних ситуациях, точность - в других. Группа часто более точна, чем индивидуум. Не менее важна сплоченность группы с признанной координационной ролью руководителя. Имеется немало ситуаций, когда решение требует многих навыков и опыта, которые не могут быть присущи одному человеку
На основе научных исследований и обширной практики принятия управленческих решений в последние десятилетия выработан целый ряд методов группового принятия решений, резко повысивших объективность и обоснованность этого процесса. Среди них - мозговая атака, метод номинальной группы, метод Дельфи.
Мозговая атака предпринимается группой как процесс генерирования идей, когда рассматриваются все возможные альтернативы с критической точки зрения.
Метод номинальной группы ограничивает обсуждения или общение друг с другом до определенного предела. Члены группы присутствуют на встрече, подействуют независимо. Вначале ставится проблема, а затем предпринимаются следующие шаги.
1. До того как начнется обсуждение, каждый независимо друг от друга записывает свои идеи поданной проблеме.
2. Проводится запись всех идей каждым членом группы.
3. Группа обсуждает идеи, чтобы их прояснить и оценить.
4. Каждый член группы независимо определяет рейтинг значимости всех идей. Окончательное решение определяется как идея с наиболее высоким совокупным рейтингом.
Основное преимущество данного метода состоит в том, что он позволяет группе формально проводить общую встречу, но не ограничивает независимость мышления каждого.
Наиболее сложным и длительным по времени является использование метода Дельфи. Он сходен с методом номинальной группы с той разницей, что физического присутствия всех членов группы не требуется. Метод Дельфи не предполагает, что членам группы придется встречаться друг с другом лицом к лицу. Этот метод характеризуют следующие шаги.
1. Определяется проблема; членов группы просят дать возможные решения посредством ответа на тщательно составленную анкету.
2. Каждый член группы анонимно и независимо отвечает на первую анкету.
3. Результаты первой анкеты собираются в центре, расшифровываются и обобщаются.
4. Каждый член группы получает копию результатов.
5. После просмотра результатов экспертов просят снова дать свои решения. Как правило, даются новые варианты решений или появляются изменения в первоначальной позиции.
6. Указанные шаги повторяются так часто, как это необходимо, пока не достигается консенсус.
Преимущество метода - независимость мнения экспертов, находящихся в пространственном отдалении друг от друга.
Промежуточное положение между групповым и индивидуальным принятием решений занимает способ, согласно которому руководитель постоянно прибегает к помощи квалифицированных консультантов перед тем, как принять решение. Он осознает необходимость консультаций и знает, как использовать потенциал группы для обоснованного и своевременного решения назревшего вопроса.
В далеком прошлом, когда еще не была придумана система исчисления, люди подсчитывали все на пальцах. С появлением арифметики и основ математики стало гораздо проще и практичнее вести учет товаров, продуктов, а также бытовых предметов. Однако как выглядит современная система исчисления: на какие виды делятся существующие числа и что значит "рациональный вид чисел"? Давайте разберемся.
Сколько разновидностей чисел существует в математике?
Само понятие "число" обозначает некую единицу любого предмета, которая характеризует его количественные, сравнительные или порядковые показатели. Для того чтобы правильно подсчитать количество определенных вещей или провести некие математические операции с числами (сложить, умножить и др.), в первую очередь следует ознакомиться с разновидностями этих самых чисел.
Итак, существующие числа можно разделить по следующим категориям:
- Натуральные - это те числа, которыми мы подсчитываем количество предметов (самое меньшее натуральное число равно 1, логично, что ряд натуральных чисел бесконечен, т. е. не существует наибольшего натурального числа). Множество натуральных чисел принято обозначать буквой N.
- Целые числа. К этому множеству относятся все при этом в него добавляются и отрицательные значения, включая число "ноль". Обозначение множества целых чисел записывают в виде латинской буквы Z.
- Рациональные числа - это те, которые мы мысленно можем преобразовать в дробь, числитель которой будет принадлежать множеству целых чисел, а знаменатель - натуральных. Чуть ниже мы разберем подробнее, что значит "рациональное число", и приведем несколько примеров.
- - множество, в которое входят все рациональные и Обозначается данное множество буквой R.
- Комплексные числа содержат в себе часть действительного и часть переменного числа. Используются в решении различных кубических уравнений, которые, в свою очередь, могут иметь в формулах под отрицательное выражение (i 2 = -1).
Что значит "рациональный": разбираем на примерах
Если рациональными считаются те числа, которые мы можем представить в виде обыкновенной дроби, то получается, что все положительные и отрицательные целые числа также входят в множество рациональных. Ведь любое целое число, например 3 или 15, можно представить в виде дроби, где в знаменателе будет единица.

Дроби: -9/3; 7/5, 6/55 - вот примеры рациональных чисел.
Что значит "рациональное выражение"?
Идем дальше. Мы уже разобрали, что значит рациональный вид чисел. Давайте теперь представим себе математическое выражение, которое состоит из суммы, разности, произведения или частного различных чисел и переменных. Вот пример: дробь, в числителе которой сумма двух или нескольких целых чисел, а знаменатель содержит в себе как целое число, так и некую переменную. Именно такое выражение и называют рациональным. Исходя из правила "на ноль делить нельзя" можно догадаться, что значение данной переменной не может быть таковым, чтобы значение знаменателя обращалось в ноль. Поэтому при решении рационального выражения следует сначала определить область значения переменной. Например, если в знаменателе следующее выражение: x+5-2, то получается, что "x" не может быть равен -3. Ведь в таком случает все выражение превращается в ноль, поэтому при решении необходимо исключить целое число -3 для данной переменной.

Как правильно решать рациональные уравнения?
Рациональные выражения могут содержать в себе довольно-таки большое количество чисел и даже 2 переменные, поэтому порой их решение становится затруднительным. Для облегчения решения такого выражения рекомендуется произвести некие операции рациональным путем. Итак, что значит "рациональным способом" и какие правила необходимо применять при решении?
- Первый вид, когда достаточно всего лишь упростить выражение. Для этого можно прибегнуть к операции сокращения числителя и знаменателя до несокращаемой величины. Например, если в числителе имеется выражение 18x, а в знаменателе 9х, то, сокращая оба показателя на 9x, получаем просто целое число, равное 2.
- Второй способ практичен тогда, когда в числителе имеем одночлен, а в знаменателе - многочлен. Разберем на примере: в числителе имеем 5x, а в знаменателе - 5x + 20x 2 . В таком случае лучше всего вынести переменную в знаменателе за скобки, получим следующий вид знаменателя: 5x(1+4x). А теперь можно воспользоваться первым правилом и упростить выражение, сократив 5x в числителе и в знаменателе. В итоге получим дробь вида 1/1+4x.

Какие действия можно выполнять с рациональными числами?
Множество рациональных чисел имеет ряд своих особенностей. Многие из них весьма схожи с характеристикой, присутствующей у целых и натуральных чисел, ввиду того что последние всегда входят в множество рациональных. Вот несколько свойств рациональных чисел, зная которые, можно с легкостью решить любое рациональное выражение.
- Свойство коммутативности позволяет суммировать два или несколько чисел, вне зависимости от их очередности. Проще говоря, от перемены мест слагаемых сумма не меняется.
- Свойство дистрибутивности позволяет решать задачи с помощью распределительного закона.
- И, наконец, операции сложения и вычитания.
Даже школьники знают, что значит "рациональный вид чисел" и каким образом решать задачи на основе таких выражений, поэтому взрослому образованному человеку просто необходимо вспомнить хотя бы азы множества рациональных чисел.
Нынешний уровень развития средств автоматизации вычислений создал у многих иллюзию о том, что развивать вычислительные навыки совсем не обязательно. Это сказалось на подготовленности школьников. При отсутствии калькулятора, даже несложные задачи вычислительного плана для многих становятся проблемой.
В то же время, экзаменационные задания и материалы по ЕГЭ содержат много задач, решение которых требует от испытуемых умений рациональной организации вычислений.
В этой статье рассмотрим некоторые способы оптимизации вычислений и их применение для задач конкурсного характера.
Наиболее часто способы оптимизации вычислений связаны с применением основных законов выполнения арифметических действий.
Например:
125 · 24 = 125 · 8 · 3 = 1000 · 3 = 3000; или
98 · 16(100 – 2) · 16 = 100 · 16 – 2 · 16 = 1600 – 32 = 1568 и т.д.
Другое направление – использование формул сокращённого умножения.
96 · 104 = (100 – 4) · (100 + 4) = 100 2 – 4 2 = 10000 – 16 = 9984; или
115 2 = (100 + 15) 2 = 10000 + 2 · 15 · 100 + 225 = 10525.
Интересным для вычислений является следующий пример.
Вычислить:
(197 ·
203 + 298 ·
302 + 13) / (1999 ·
2001 + 2993 ·
3007 + 50) =
= ((200 – 3) ·
(200 + 3) + (300 – 2) ·
(300 + 2) + 13) / ((2000 – 1) ·
(2000 + 1) + (3000 – 7) ·
(3000 + 7) + 50) =
= (200 2 – 3 2 + 300 2 – 2 2 + 13) / (2000 2 – 1 2 + 3000 2 – 7 2 – 50) =
= 130000 / 13000000 = 0,01
Это практически стандартные способы оптимизации вычислений. Иногда предлагаются и более экзотические. В качестве примера рассмотрим способ умножения двухзначных чисел, сумма единиц у которых равна 10.
54 · 26 = 50 · 30 + 4 · (26 – 50) = 1500 – 96 =1404 или
43 · 87 = 40 · 90 + 3 · (87 – 40) = 3600 + 141 = 3741.
Схему умножения можно понять из рисунка.
Откуда получается такая схема умножения?
Наши числа по условию имеют вид: M = 10m + n, K = 10k + (10 – n). Составим произведение:
M · K = (10m + n)(10k + (10 – n)) =
= 100mk + 100m – 10mn + 10nk + 10n – n 2 =
= m(k + 1) · 100 + n(10k + 10 – n) =
= (10m) · (10 · (k + 1)) + n · (K – 10m) и способ обоснован.
Можно привести множество хитроумных способов превращения достаточно сложных вычислений в устные задачи. Но нельзя думать, что всем необходимо запоминать эти и еще кучу других хитроумных способов упрощения вычислений. Важно лишь усвоить некоторые базовые из них. Разбор же других имеет смысл лишь для выработки навыков применения базовых способов. Именно их творческое применение и дает возможность достаточно быстро и правильно решать задачи вычислительного характера.
Иногда при решении примеров на вычисление удобно перейти от преобразования выражения с числами к преобразованию многочленов. Рассмотрим следующий пример.
Вычислить наиболее рациональным способом:
3 1 / 117 · 4 1 / 110 -1 110 / 117 · 5 118 / 119 - 5 / 119
Решение.
Пусть а = 1 / 117 и b = 1 / 119 . Тогда 3 1 / 117 = 3 + а, 4 1 / 119 = 4 + b, 1 116 / 117 = 2 – а, 5 118 / 119 = 6 – b.
Таким образом, заданное выражение можно записать в виде (3 + а) · (4 + b) – (2 – а) · (6 – b) – 5b.
Выполнив несложные преобразования многочлена, получим 10a или 10 / 117 .
Здесь мы получили, что значение нашего выражения не зависит от b. А это означает, что мы вычислили не только значение данного выражения, но и любого другого, полученного из (3 + а) · (4 + b) – (2 – а) · (6 – b) – 5b путем подстановки значений a и b. Если, к примеру, a = 5 / 329, то в ответе получим 50 / 329 , каким бы не было b.
Рассмотрим ещё один пример, решение которого с помощью калькулятора практически невозможно, а ответ довольно прост, если знаешь подход к решению примеров такого типа
Вычислить
1 / 6 · 7 1024 – (7 512 + 1) · (7 256 + 1) · (7 128 + 1) · (7 64 + 1) · (7 32 + 1) · (7 16 + 1) · (7 8 + 1) · (7 4 + 1) · (7 2 + 1) · (7 + 1)
Решение.
Преобразуем условие
1 / 6 · 7 1024 - 1 / 6 · (7 512 + 1) · (7 256 + 1) · (7 128 + 1) · (7 64 +1) · (7 32 + 1) · (7 16 + 1) · (7 8 + 1) · (7 4 + 1) · (7 2 + 1) · (7 + 1) · (7 – 1) =
1 / 6 · 7 1024 - 1 / 6 (7 512 + 1) · (7 256 + 1) · (7 128 + 1) · (7 64 + 1) · (7 32 + 1) · (7 16 + 1) · (7 8 + 1) · (7 4 + 1) · (7 2 + 1) · (7 2 – 1) =
1 / 6 · 7 1024 - 1 / 6 (7 512 + 1) · (7 256 + 1) · (7 128 + 1) · (7 64 + 1) · (7 32 + 1) · (7 16 + 1) · (7 8 + 1) · (7 4 + 1) · (7 4 – 1) =
1 / 6 · 7 1024 - 1 / 6 (7 512 + 1) · (7 256 + 1) · (7 128 + 1) · (7 64 + 1) · (7 32 + 1) · (7 16 + 1) · (7 8 + 1) · (7 8 – 1) =
1 / 6 · 7 1024 - 1 / 6 (7 512 + 1) · (7 256 +1) · (7 128 + 1) · (7 64 + 1) · (7 32 + 1) · (7 16 + 1) · (7 16 – 1) = … =
1 / 6 · 7 1024 - 1 / 6 (7 512 + 1) · (7 512 – 1) = 1 / 6 · 7 1024 - 1 / 6 · (7 1024 – 1) = 1 / 6
Рассмотрим один из примеров, ставший уже хрестоматийным в экзаменационных материалах за курс базовой школы.
Вычислить сумму:
1/2 + 1 / (2 · 3) + 1 / (3 · 4) + 1 / (4 · 5) + … + 1 / (120 · 121) =
= (1 – 1/2) + (1/2 – 1/3) + (1/3 – 1/4) + (1/4 – 1/5) + … + (1/120 – 1/121) =
= 1 – 1/121 = 120/121.
То есть решить данную задачу позволил способ замены каждой дроби разностью двух дробей. В сумме оказались пары противоположных чисел всем, кроме первого и последнего.
Но этот пример можно обобщить. Рассмотрим сумму:
k/(n · (n + k)) + k/((n + k) · (n + 2k)) + k/((n + 2k) · (n + 3k)) + … + k/((n + (m – 1)k) · (n + mk))
Для нее справедливы все те же рассуждения, которые проведены в предыдущем примере. В самом деле:
1/n – 1/(n + k) = k/(n · (n + k));
1/((n + k) – 1/(n + 2k) = k/((n + k) · (n + 2k)) и т.д.
Тогда ответ построим по той же схеме: 1/n – 1/(n + mk) = mk/(n · (n + mk))
И еще о «длинных» суммах.
Сумму
Х = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024
можно вычислить как сумму 11 членов геометрической прогрессии со знаменателем 1/2 и первым членом 1. Но эту же сумму может вычислить и ученик 5 класса, не имеющий представления о прогрессиях. Для этого достаточно удачно подобрать число, которое добавим до суммы Х. Таким числом здесь окажется 1/1024.
Вычислим
Х + 1 / 1024 = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + (1/1024 + 1/1024) =
= 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/512 =
=1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/256 = … = 1 + 1/2 + 1/2 = 2.
Теперь очевидно, что Х = 2 – 1/1024 = 1 1023 / 1024 .
Второй способ не менее перспективен. С его помощью можно вычислить сумму:
S = 9 + 99 + 999 + 9999 + … + 99 999 999 999.
Здесь «удачное» число 11. Добавляя его к S и распределим равномерно между всеми 11 слагаемыми. Каждому из них тогда достанется по 1. Тогда имеем:
S + 11 = 9 + 1 + 99 + 1 + 999 + 1 + 9999 + 1 + … + 99 999 999 999 + 1 =
= 10 + 100 + 1000 + 10000 + ... + 100 000 000 000 = 111 111 111 110;
Следовательно, S = 111 111 111 110 – 11 = 111 111 111 099.
1 + 11 + 111 + 1111 + ... + 1 111 111 111?
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Смотрим в словаре, что же такое рациональное решение – это: 1) продуманное, взвешенное решение, принятое на основе сравнения вариантов и их выбора, а также учета еще многих факторов; 2) выгодное, целесообразное решение.
Иногда на уроках при решении заданий учеником выясняется, что он вообще не знает, что такое рациональное решение . Оказывается, что такое решение связано с недостаточными познаниями ученика.
Задача.
Однажды на уроке математики учитель показал ребятам куб и предложил найти площадь поверхности этого куба.
— Это элементарно, — поднял первым руку Петя Самохвалов. – Сначала измеряем два ребра, исходящие из одной вершины. Первое ребро равно 10 см, и второе ребро равно 10 см. Найдем площадь этой грани: 10 х 10 = 100 (см 2). Теперь измерим другие два ребра. Первое равно 10 см, и второе равно 10 см. Перемножим их, будет 100 см 2 . Это площадь второй грани…
Потом Петя точно также нашел площадь четырех оставшихся граней. Все они оказались равными 100 см 2 .
— Теперь, продолжал Петя, сложим все найденные площади, будет 600 см 2 . Это и есть площадь поверхности куба.
Как же Петя был удивлен, когда учитель не поставил ему пятерку. Как вы думаете почему?
Иногда не находя выгодное, рациональное решение ученик заходит в такие дебри, что уже и сам запутывается.
Был такой случай на уроке математики
:
Ученик решал задачу
у доски. При не правильно выбранном, не рациональном решении он уже исписал почти всю доску. Учитель очень серьезно двух ребят посильнее и покрепче, попросила из соседнего свободного на данный момент класса принести еще одну доску. Не сознавая подвоха, ребята встали и пошли к выходу. Когда они дошли уже до двери, учитель сказала:
— Возможно нужно будет принести и две доски… Ученику, решающему задачу
у доски места катастрофически не хватает…
Вот тут-то все всё и поняли. Посмеялись от души.
И еще одна задача:
Двое шли — рубль нашли.
Четверо пойдут — сколько найдут?