Множество значений функции определение. Нахождение множества значений функции

Функция - одно из важнейших математических понятий.

Определение: Если каждому числу из некоторого множества x поставлено в соответствие единственное число y, то говорят, что на этом множестве задана функция y(x). При этом x называют независимой переменной или аргументом, а y - зависимой переменной или значением функции или простофункцией.

Говорят также, что переменная y является функцией от переменной x.

Обозначив соответствие некоторой буквой, например f, удобно писать: y=f (x), то есть, значение y получается из аргумента x с помощью соответствия f. (Читают: y равно f от x.) Символом f (x) обозначают значение функции, соответствующее значению аргумента, равному x.

Пример 1 Пусть функция задается формулой y=2x 2 –6. Тогда можно записать, что f(x)=2x 2 –6. Найдем значения функции для значений х, равных, например, 1; 2,5;–3; т. е. найдем f(1), f(2,5), f(–3):

f(1)=2 1 2 –6=–4;
f(2,5)=2 2,5 2 –6=6,5;
f(–3)=2 (–3) 2 –6= 12.

Заметим, что в записи вида y=f (x) вместо f употребляют и другие буквы: g, и т. п.

Определение: Область определения функции - это все значения x, при которых существует функция.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.

Определение: Все значения, которые принимает зависимая переменная образуют область значения функции.

Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой, где l 0 начальная длина стержня, а -коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функцииl=g(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.

Пример.

Укажите область значений функции y = arcsinx .

Решение.

Областью определения арксинуса является отрезок [-1; 1] . Найдем наибольшее и наименьшее значение функции на этом отрезке.

Производная положительна для всех x из интервала (-1; 1) , то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1 , а наибольшее при x = 1 .

Мы получили область значений функции арксинуса .

Найдите множество значений функции на отрезке .

Решение.

Найдем наибольшее и наименьшее значение функции на данном отрезке.

Определим точки экстремума, принадлежащие отрезку :

Функция y=f(x) — это такая зависимость переменной y от переменной x , когда каждому допустимому значению переменной x соответствует единственное значение переменной y .

Областью определения функции D(f) называют множество всех допустимых значений переменной x .

Область значений функции E(f) — множество всех допустимых значений переменной y .

График функции y=f(x) — множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек, вида M (x; f(x)) . График функции представляет собой некоторую линию на плоскости.

Если b=0 , то функция примет вид y=kx и будет называться прямой пропорциональностью .

D(f) : x \in R;\enspace E(f) : y \in R

График линейной функции — прямая.

Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:

k= tg \alpha , где \alpha — угол наклона прямой к положительному направлению оси Ox .

1) Функция монотонно возрастает при k > 0 .

Например: y=x+1

2) Функция монотонно убывает при k < 0 .

Например: y=-x+1

3) Если k=0 , то придавая b произвольные значения, получим семейство прямых параллельных оси Ox .

Например: y=-1

Обратная пропорциональность

Обратной пропорциональностью называется функция вида y=\frac {k}{x} , где k — отличное от нуля, действительное число

D(f) : x \in \left \{ R/x \neq 0 \right \}; \: E(f) : y \in \left \{R/y \neq 0 \right \} .

Графиком функции y=\frac {k}{x} является гипербола.

1) Если k > 0 , то график функции будет располагаться в первой и третьей четверти координатной плоскости.

Например: y=\frac{1}{x}

2) Если k < 0 , то график функции будет располагаться во второй и четвертой координатной плоскости.

Например: y=-\frac{1}{x}

Степенная функция

Степенная функция — это функция вида y=x^n , где n — отличное от нуля, действительное число

1) Если n=2 , то y=x^2 . D(f) : x \in R; \: E(f) : y \in ; основной период функции T=2 \pi

ГБОУ лицей (экономический) с. Исаклы

Учитель математики Кузаева В.Н.

2016 год

Справочные материалы

Образец решения Найти множество значений функций

Область значения функции
является

y - любое число

Область значения функции
является y - любое число

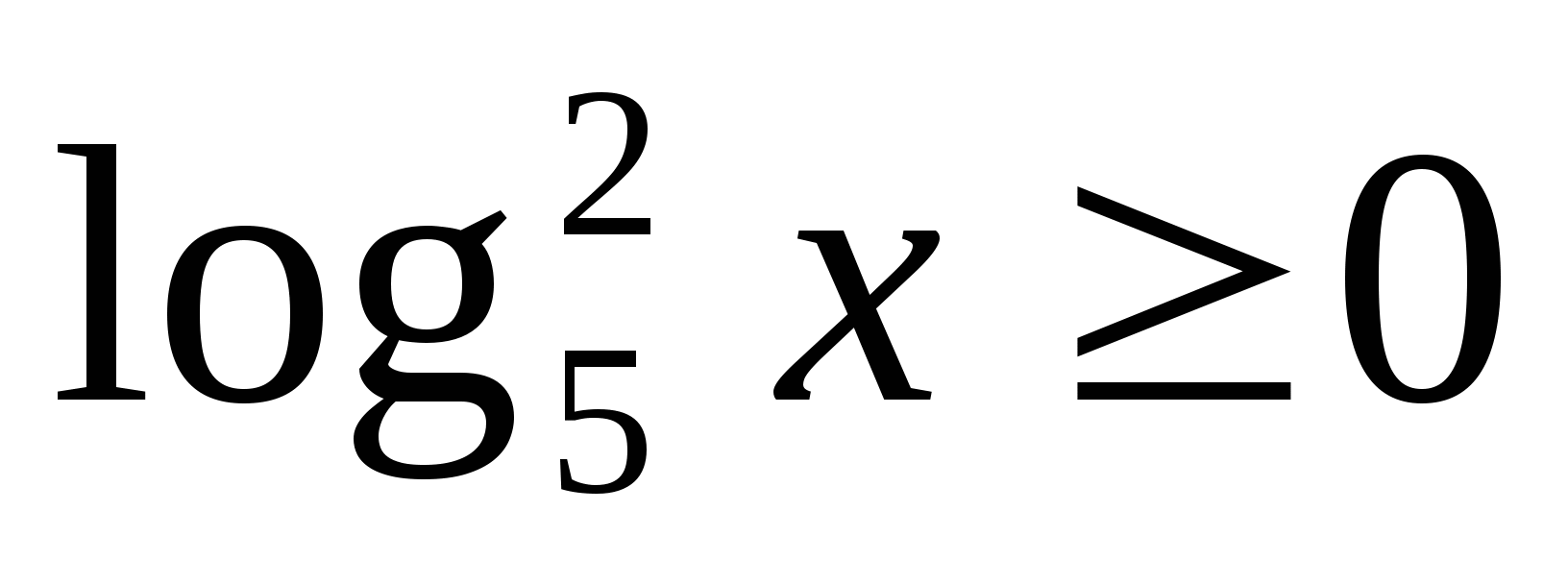
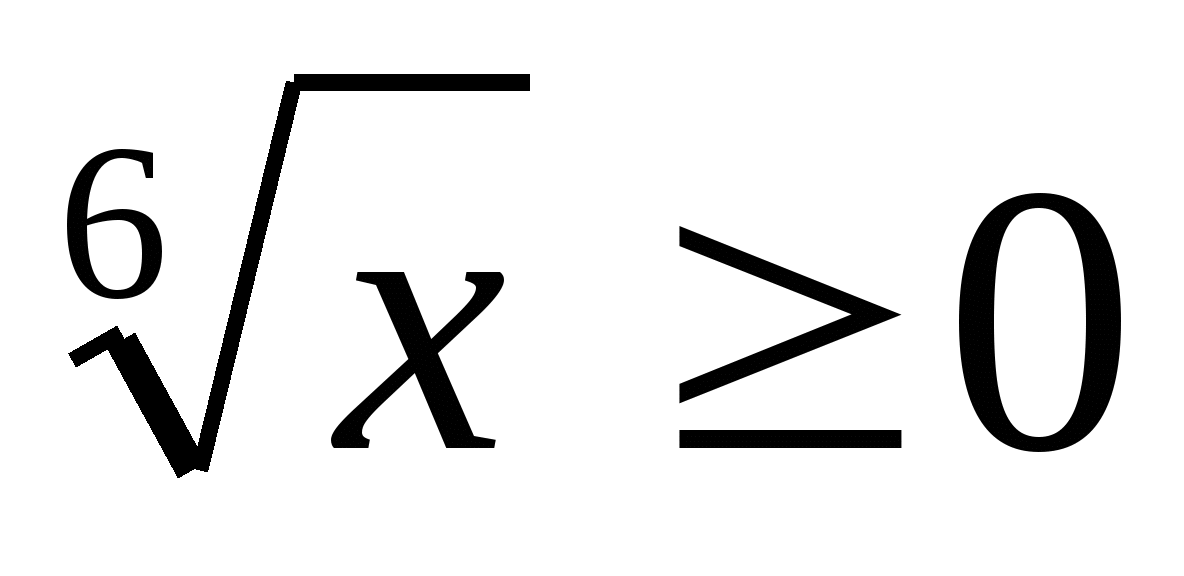
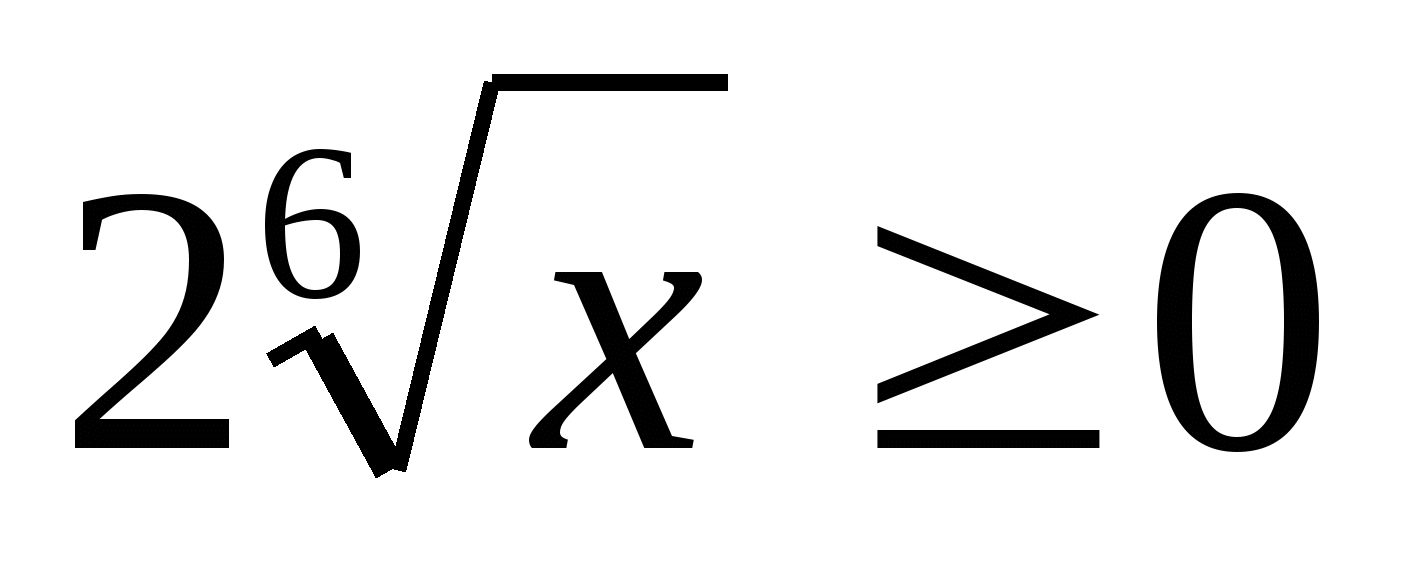
Множество значений

y - любое число

Наибольшее значение

Наименьшее значение

Область определения х - любое число
, где

, где

Множество значений
y - любое число y - любое число


Шаблоны графиков некоторых тригонометрических функций

Множество значений тригонометрических функций

Вариант 1

У = sin 3х+2.

1) (-5;5) 2) 3) 4) (1;5)

2. Найдите область значения функции у = tg х + 1.

1) 3) (-∞;∞) 4)


1) -6 2) 6 3) -4 4) -2

4. Укажите наименьшее целое число из области значений функции

у = 12,7 + 5 sin (3х-2).

1) -5 2) 8 3) 5 4) 17

5. Укажите функцию, множеством значений которой является отрезок [-2;2].

1) у = cos 2х 2) у = sin 2 x 3) y = cos 2 x +2

4) y = 2 sin 4 x

6. Найдите множество значений функции y = tg 2 x на отрезке




7. Найдите сумму всех целых чисел, которые входят в область значений функции y = 4 cos 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Вариант 2

y = 2 cos 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Найдите область значения функции

1) 3) (-∞;∞) 4) .

3. Укажите наименьшее число из области значений функции

1) 4 2) -3 3) 1 4) -7

4. Укажите наибольшее целое из области значений функции

1) 2 2) 13 3) 12 4) -2

5. Укажите функцию, множеством значений которой является отрезок [-5;5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Найдите множество значений функции
на отрезке




7. Найдите произведение всех целых чисел, которые входят в область значений функции у = 5 – 3 sin 2 x .

1) 120 2) 14 3) -15 4) 0

Вариант 3
1. Укажите множество значений функции y = sin 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)


1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Укажите наименьшее число из области значений функции у = 5 tg 2 x +2?

1) 5 2) 0 3) 7 4) 2


1) -1 2) -2,7 3) -2,3 4)-3

5. Укажите функцию, множеством значений которой является отрезок

[-17;-13].

1) y = 5 sin x – 8 3) y = -cos x +15

2) y = 2 cos x – 15 4) y = 3 sin x +10

6. Укажите наименьшее натуральное число, которое не входит в множество значений функции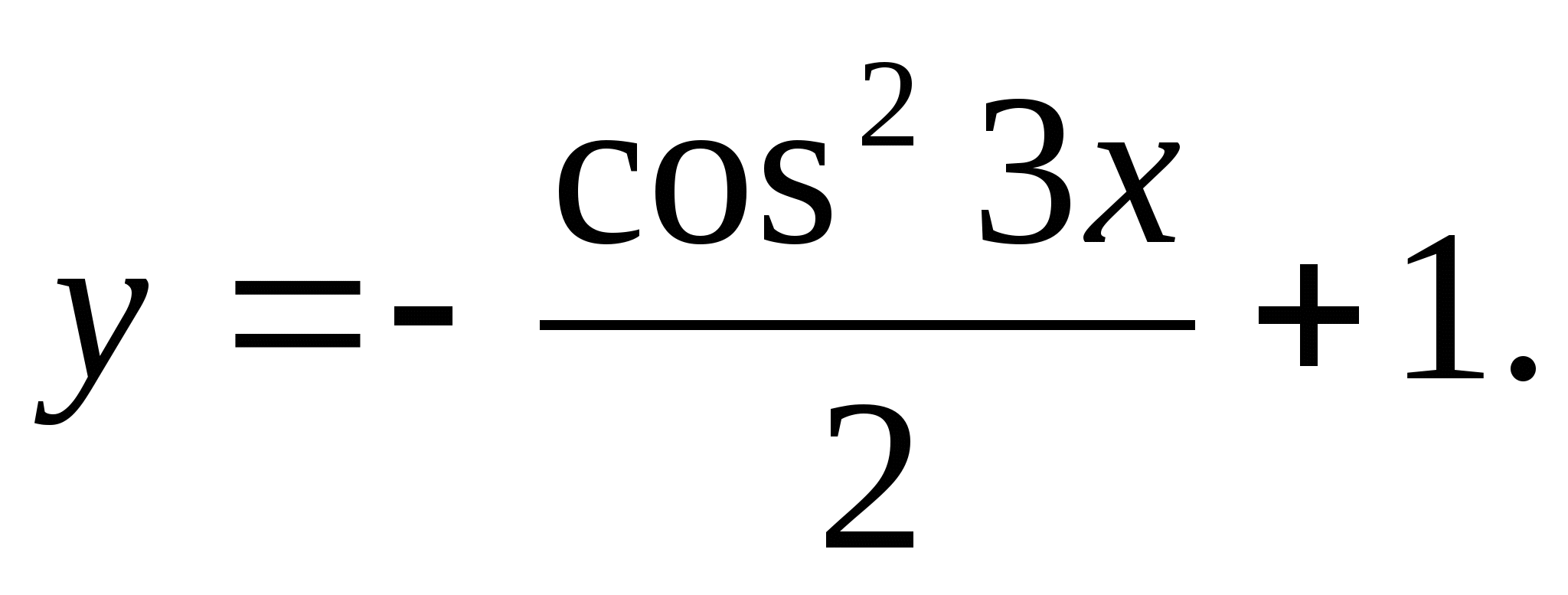

1) 2 2) 4 3) 15 4) 6

7. Сколько целых чисел принадлежит множеству значений функции

y = 2 cos 3 x +10?

1) 2 2) 3 3) 4 5) 5

Вариант 4


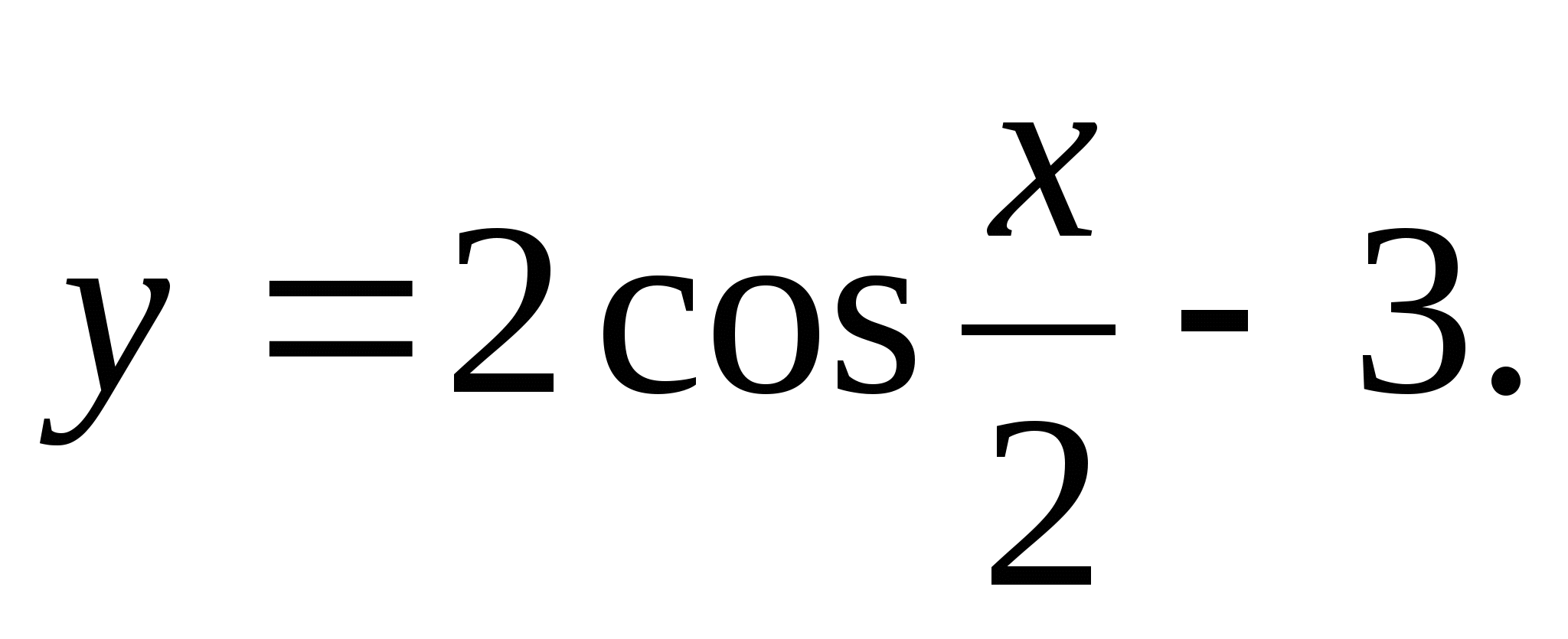
1) 2) 4) (-7;-6)

2. Найдите область значений функции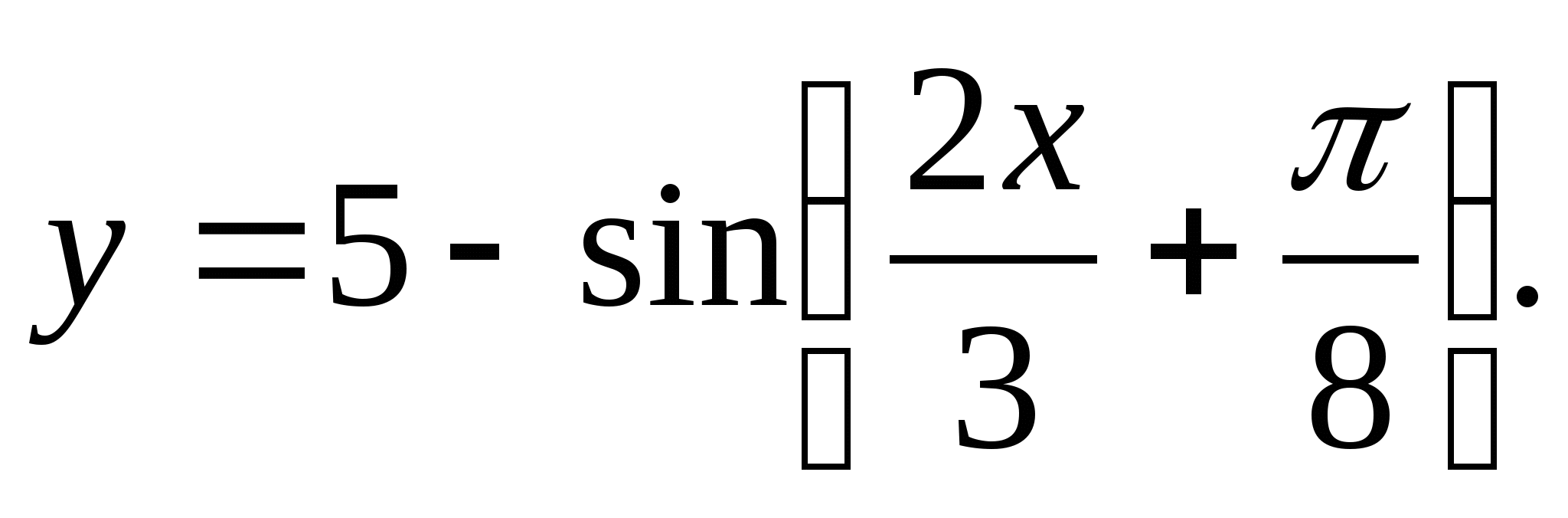

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Укажите наибольшее число из области значений функции y = -3 ctg 2 x +7.

1) 10 2) 4 3) 7 4) -3

4. Какое из следующих чисел не входит в множество значений функции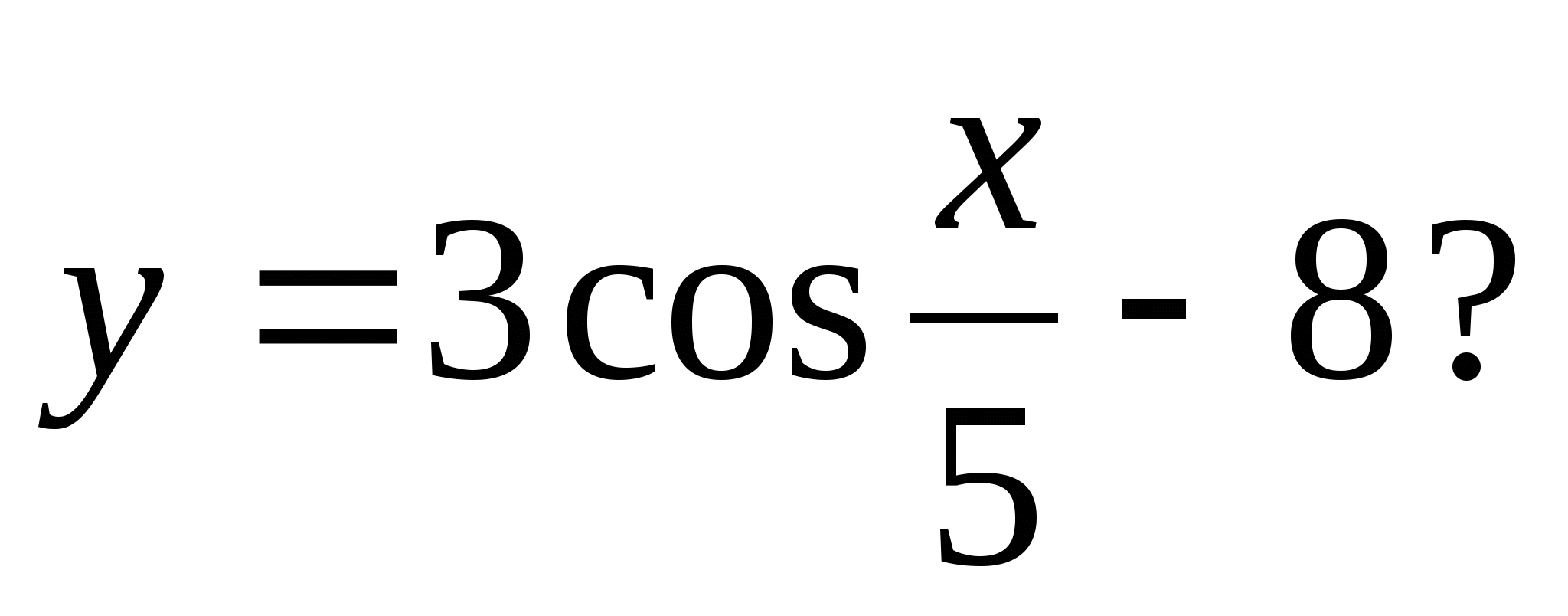

1) -6 2) -5 3) -10 4) -7

5. Укажите функцию, множеством значений которой является отрезок .



6. Укажите наибольшее целое отрицательное число, которое не входит в область значений функции

1) -1 2) -25 3) -6 4) -2

7. Сколько целых чисел принадлежит множеству значений функции

1) 11 2) 3 3) 5 4) 4

Вариант 5

1. Укажите множество значений функции у = 2 - sin 5 x .

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Найдите область значений функции

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Укажите наименьшее целое число из области значений функции

y = 3 + sin 2 2 x .

1) 0 2) 1 3) 3 4) 4

4. Какое из следующих чисел входит в множество значений функции

1) 128 2) 10,5 3) 3 4) -235

5. Укажите функцию, множеством значений которой является отрезок [-9;15].



6. Найдите сумму целых чисел, входящих в множество значений функции

1) 0 2) 7 3) 18 4) 22

7. Найдите наибольшее значение функции
на отрезке

1) 0,5 2) 1,5 3) 0 4) 2

Вариант 6

1. Укажите отрезок, соответствующий множеству значений функции

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Найдите область значений функции

3. Укажите наибольшее число из области значений функции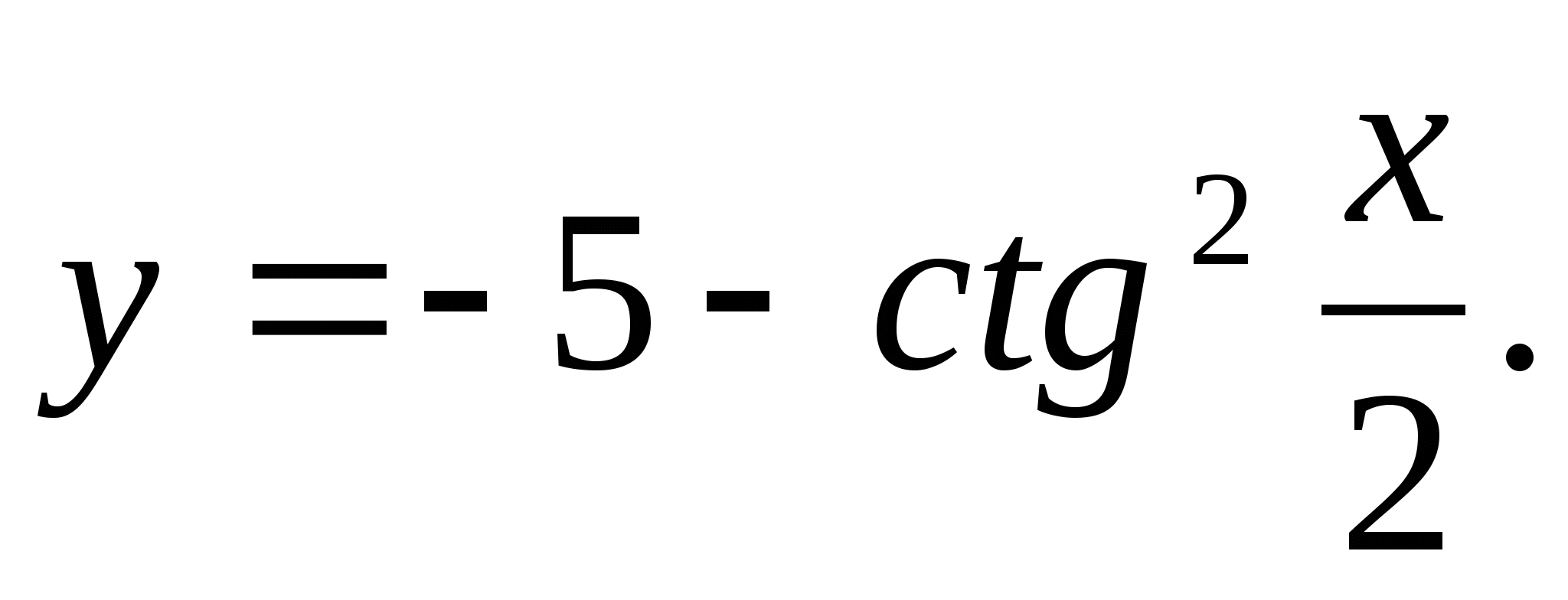

1) 5 2) -6 3) -3 4) 4

4. Какое из следующих чисел входит в множество значений функции

1) 5 2) 0 3) -3 4) 4

5. Укажите функцию, множество значений которой является отрезок .

1) у = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 cos 4 x 4) y = - tg 2 x + 1

6. Найдите произведение целых чисел, входящих в множество значений

y = 3,8 – 1,4 sin 3 x .

1) 17 2) 12 3) 0 4) 60

7. Найдите множество значений функции
на промежутке

1) (3;4) 2) 3)

Вариант 7





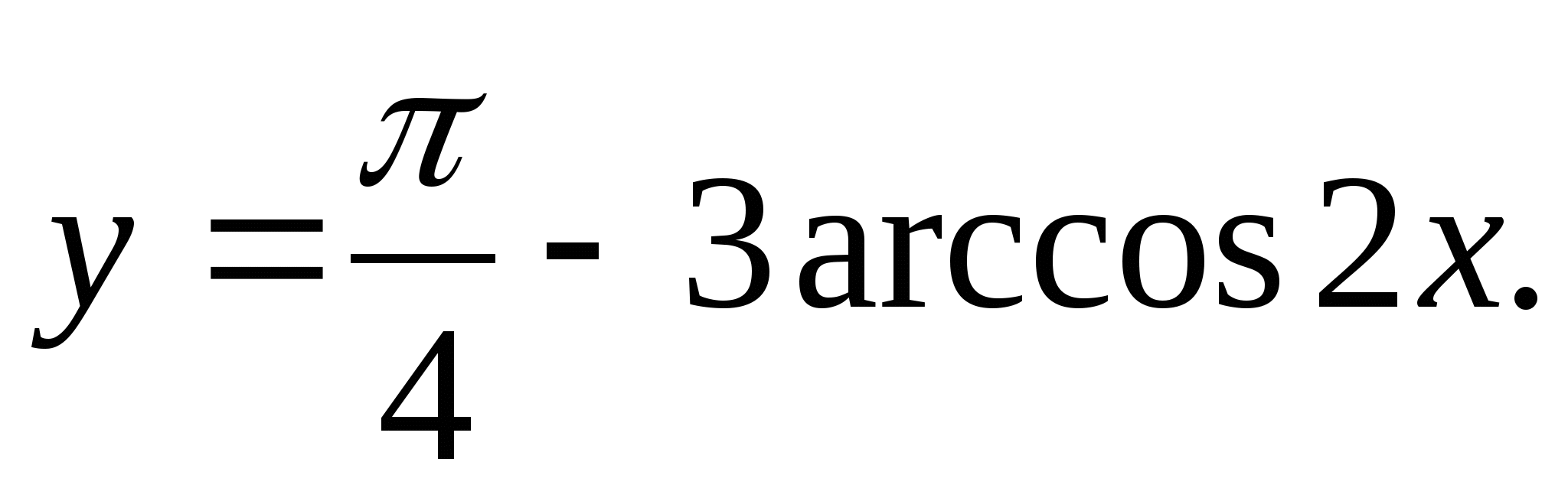
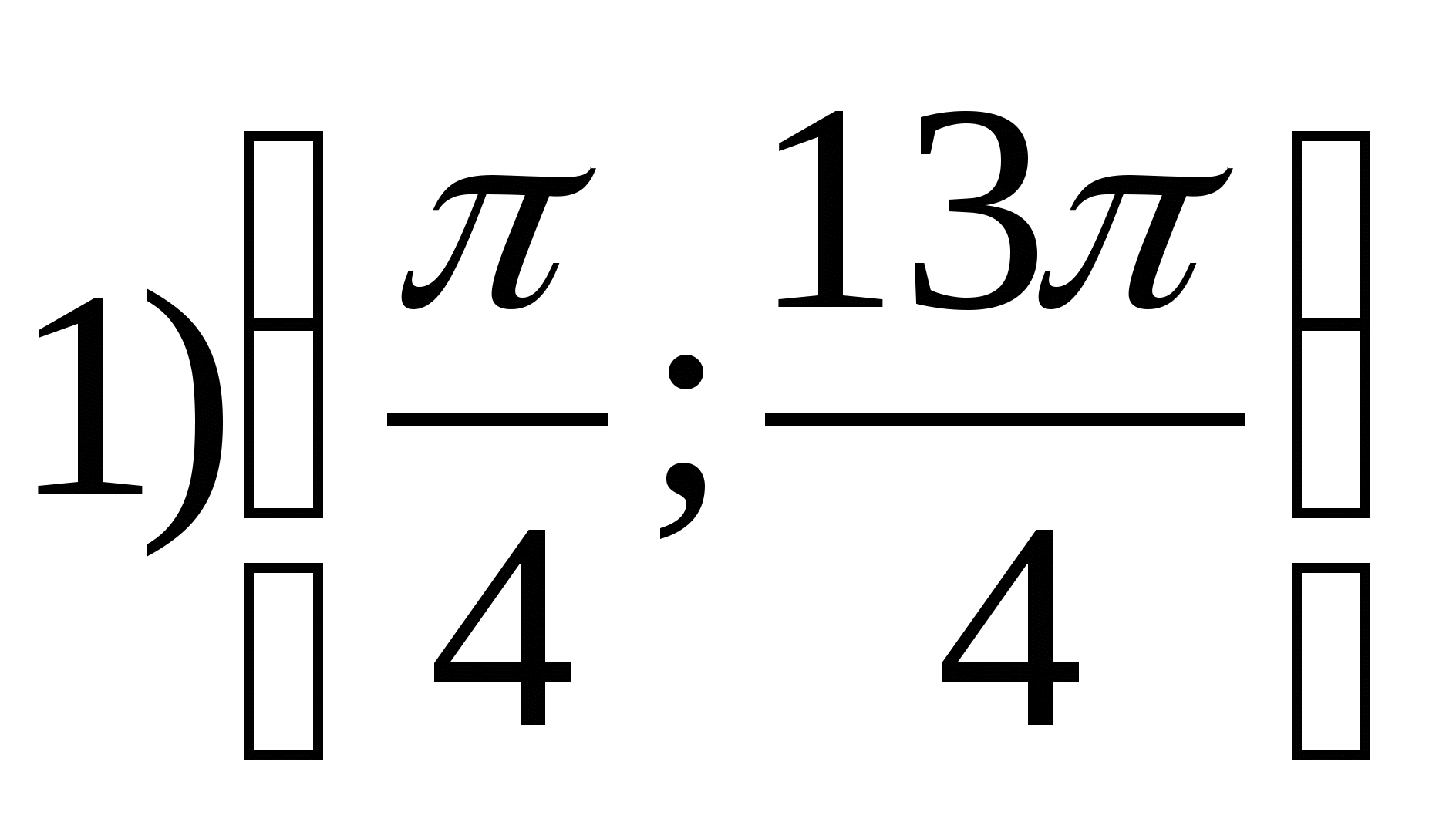
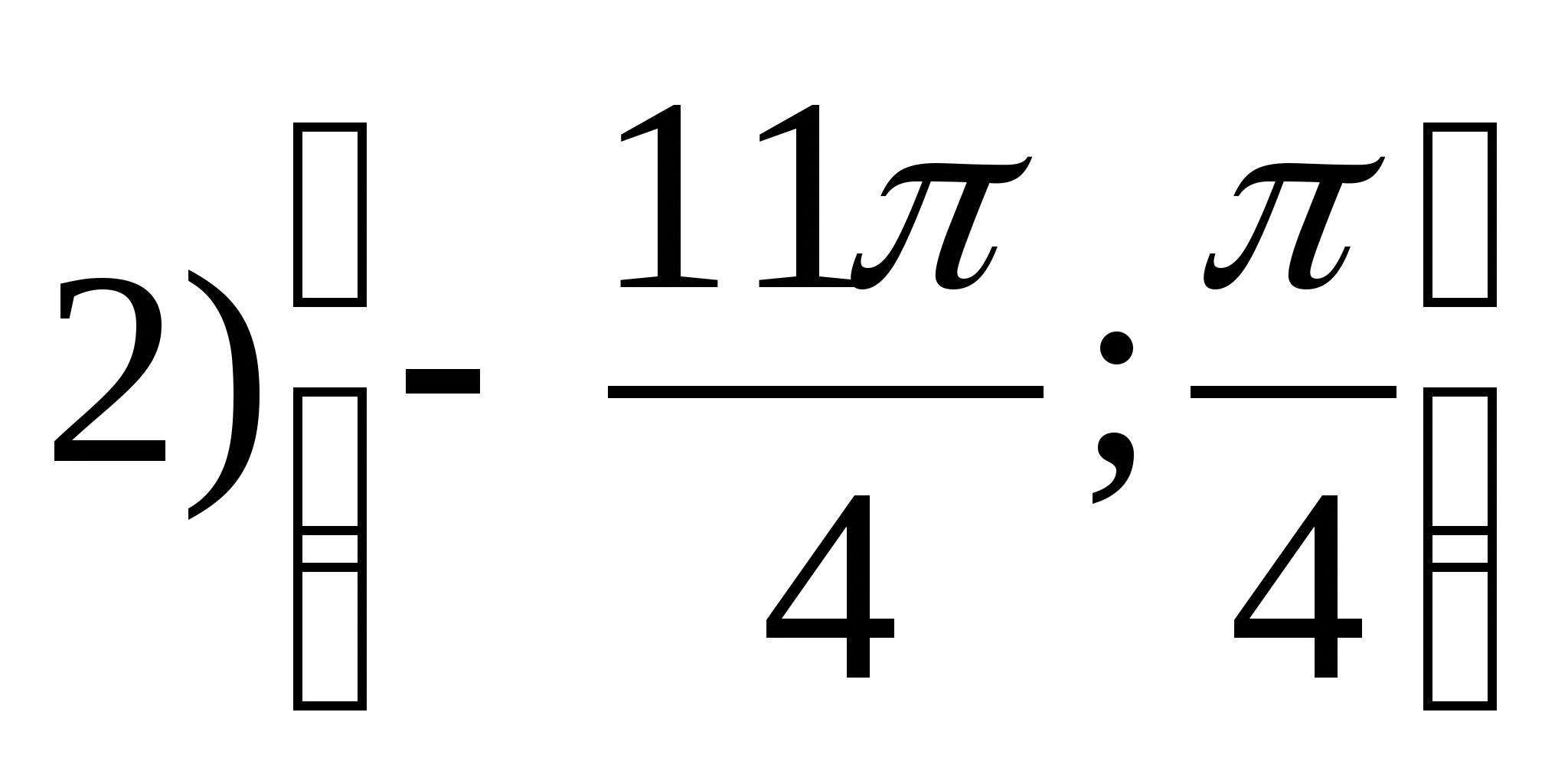
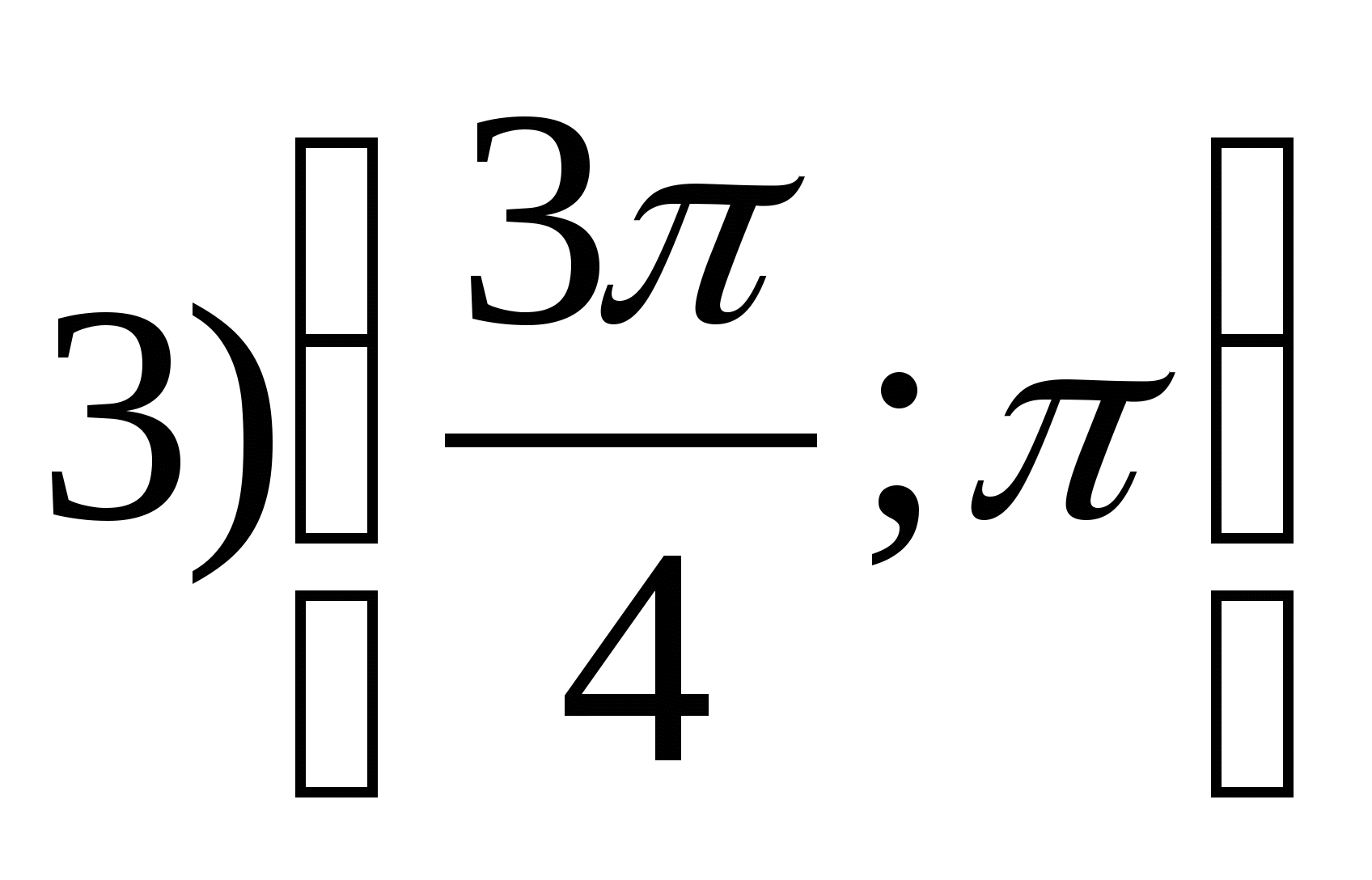
2. Найдите наименьшее целое значение функции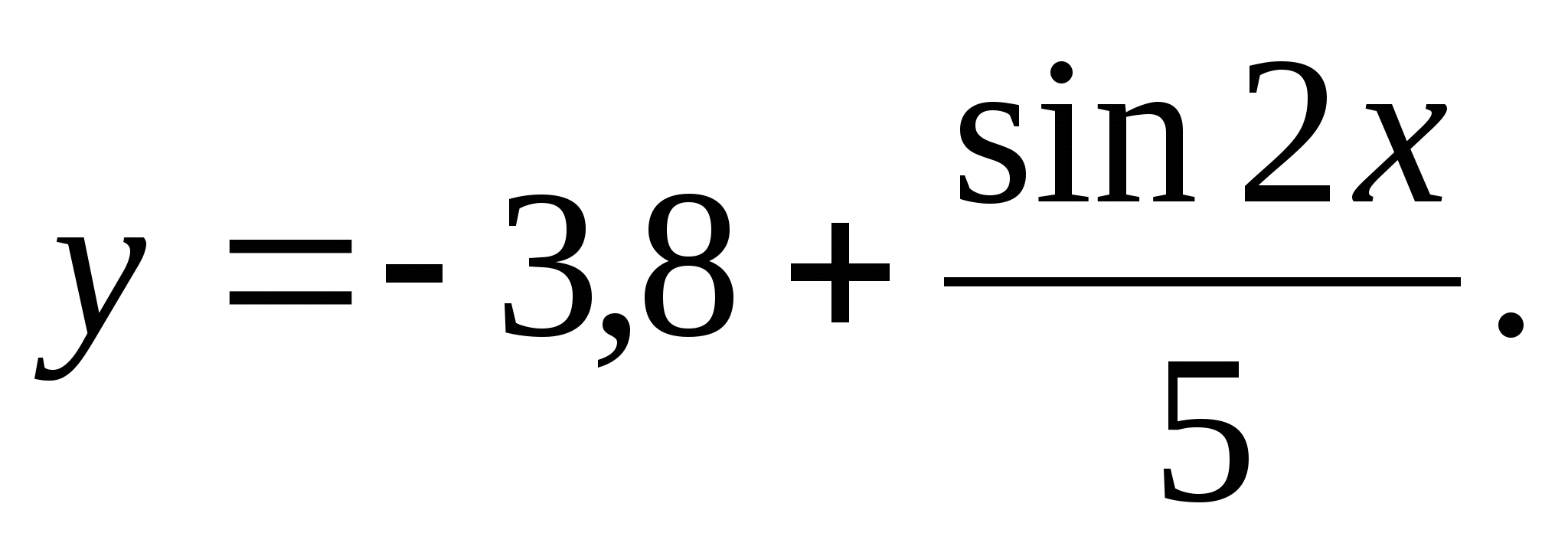

1) 2 2) 0 3) -3 4) -4


1) 0 2) 2 3) 4 4) 6

4. При каких значениях а уравнение sin (3 x -4)+5= a разрешимо?

1) 2) 3) (4;6) 4) (-6;4]

sin 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]


на промежутке

2) 0 3) 1

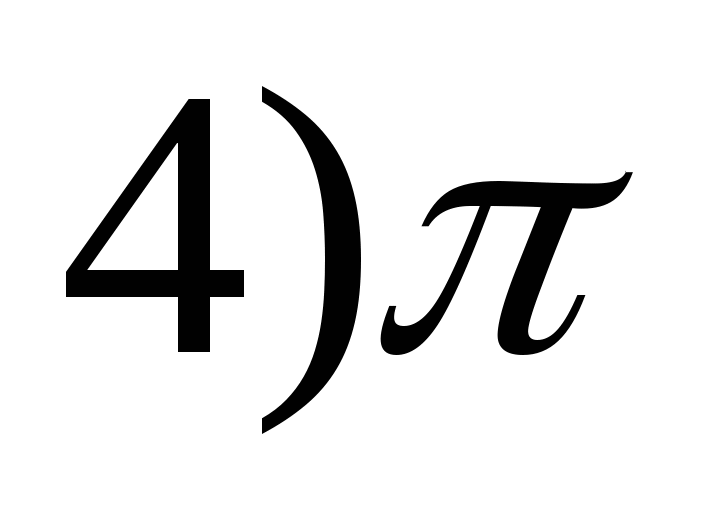
y = 4 sin (x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Вариант 8

1. Найдите множество значений функции y = arctg x - 2π.




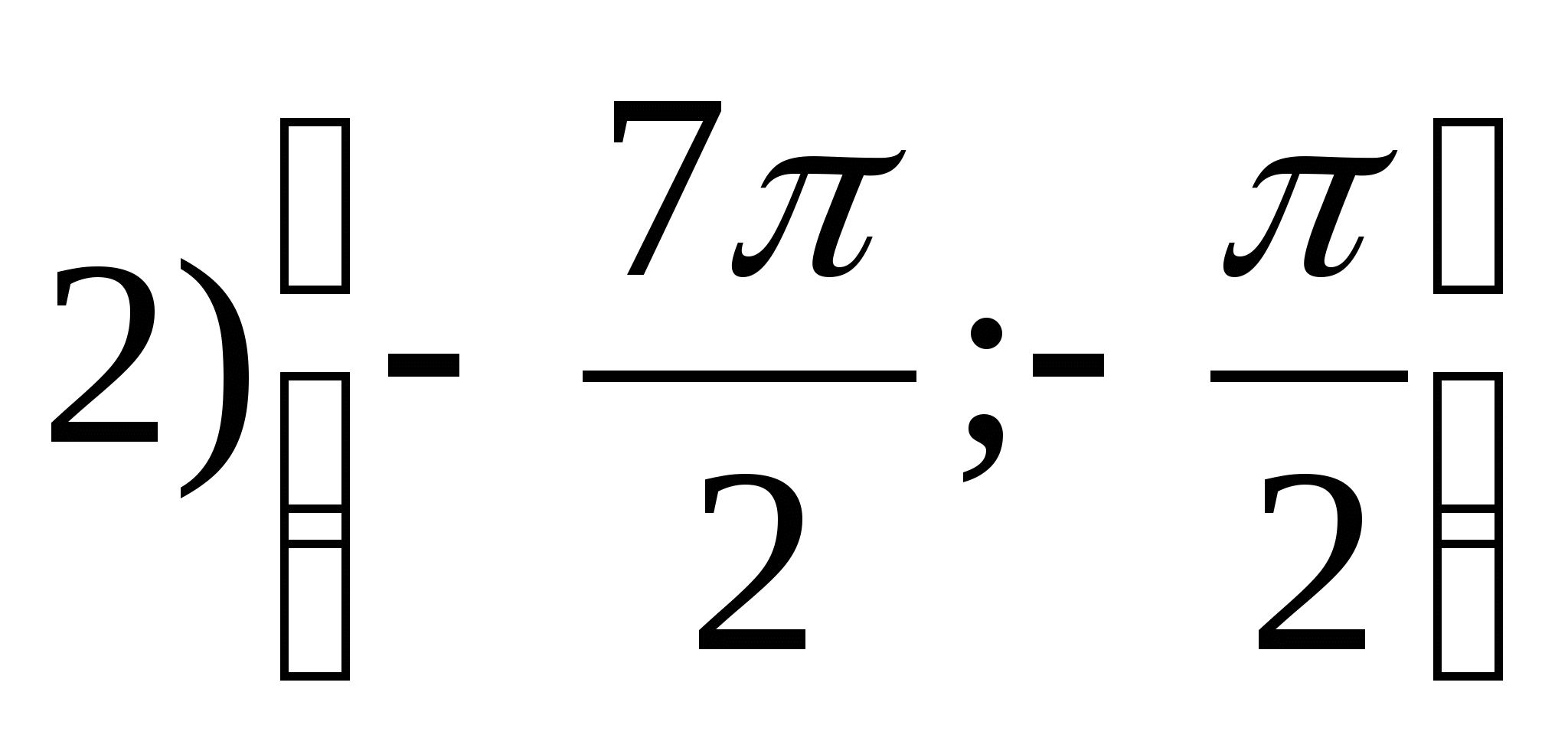
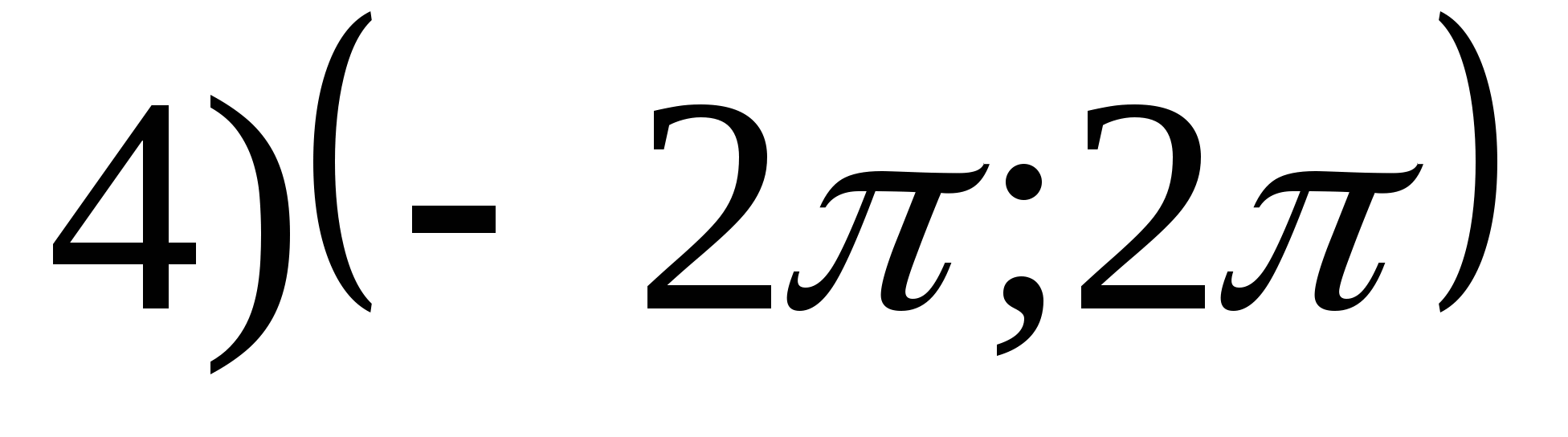
2. Найдите наибольшее значение функции

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Какое из следующих чисел может быть значением функции

1) -4 2) -2 3) 0 4) 2

4. При каких значениях р уравнение -2+ cos (4 x -1)= p имеет корни?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Найдите множество значений функции y = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)


на промежутке
.

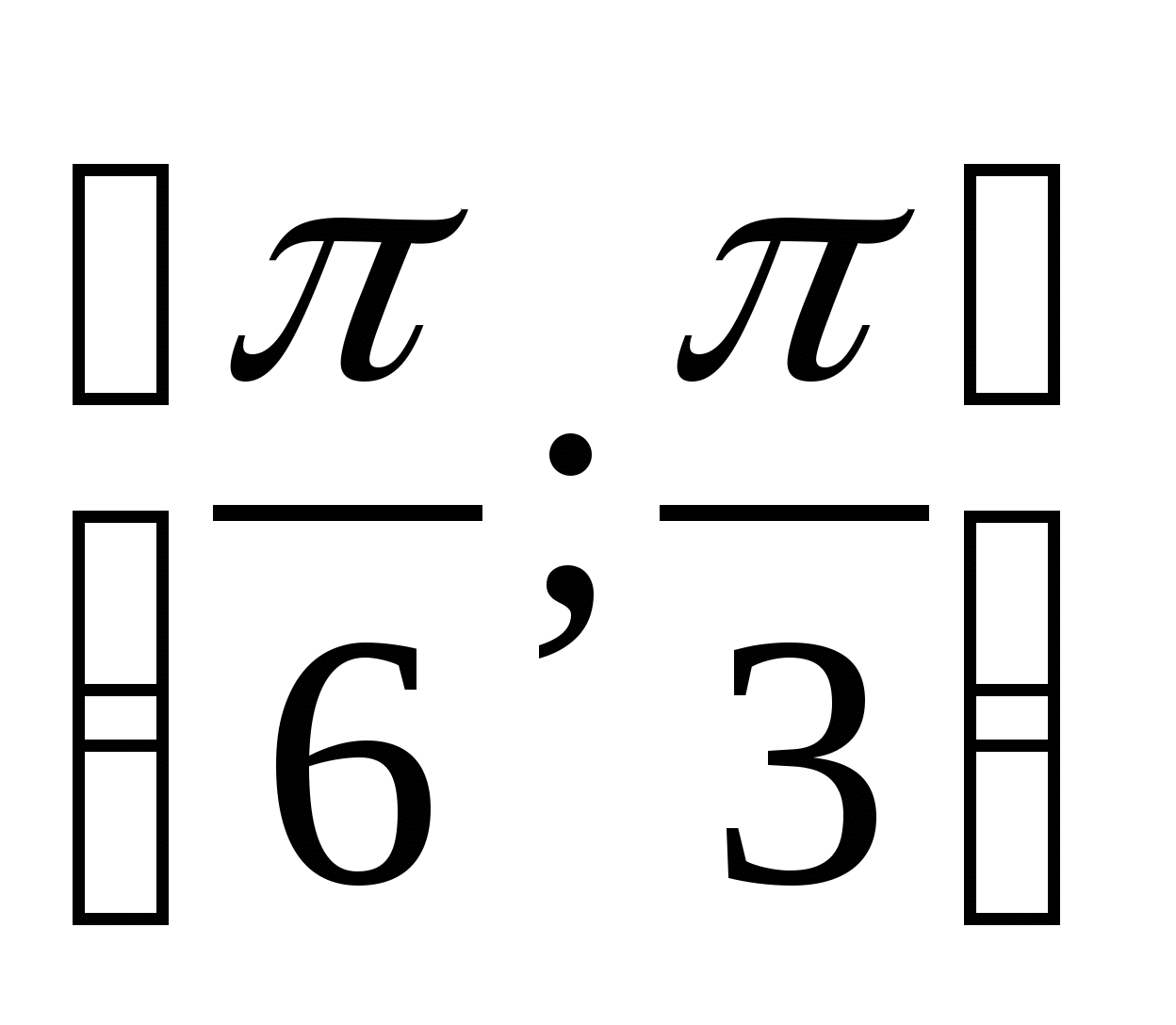1) 0 2) 1 3) -1 4) 3

7. Сколько целых чисел принадлежит области значений функции

1) 4 2) 3 3) 5 4) 2

Вариант 9

1. Найдите область значений функции




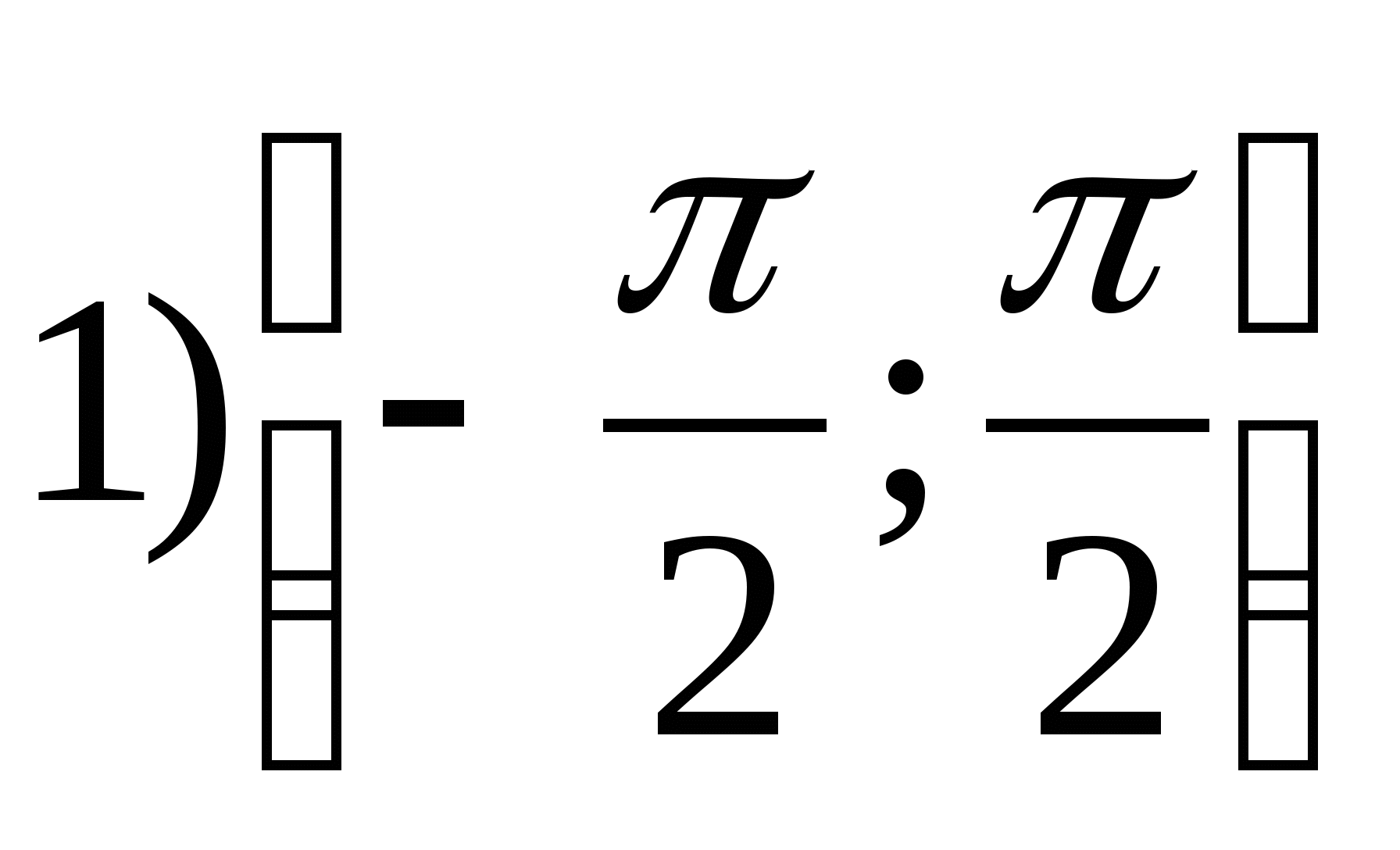
2. Найдите наибольшее целое значение функции

1) 4 2) 5 3) 6 4) 7

3. Какое из следующих чисел может быть значением функции

1) 0 2) 3 3) 6 4) 9

k уравнение – k + sin (2 x -1) = 2 разрешимо?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Найдите множество значений функции у = - cos 2 3 x + 4.

1) 2) 3) 4)

6. Укажите наименьшее значение функции
на промежутке

2) -1 3) 0 4) 1

7. Найдите, сколько целых чисел входит в область значений функции у = 12 cos 3 x +5 sin 3 x .

1) 13 2) 27 3) 26 4) 14

Вариант 10

1. Найдите область значений функции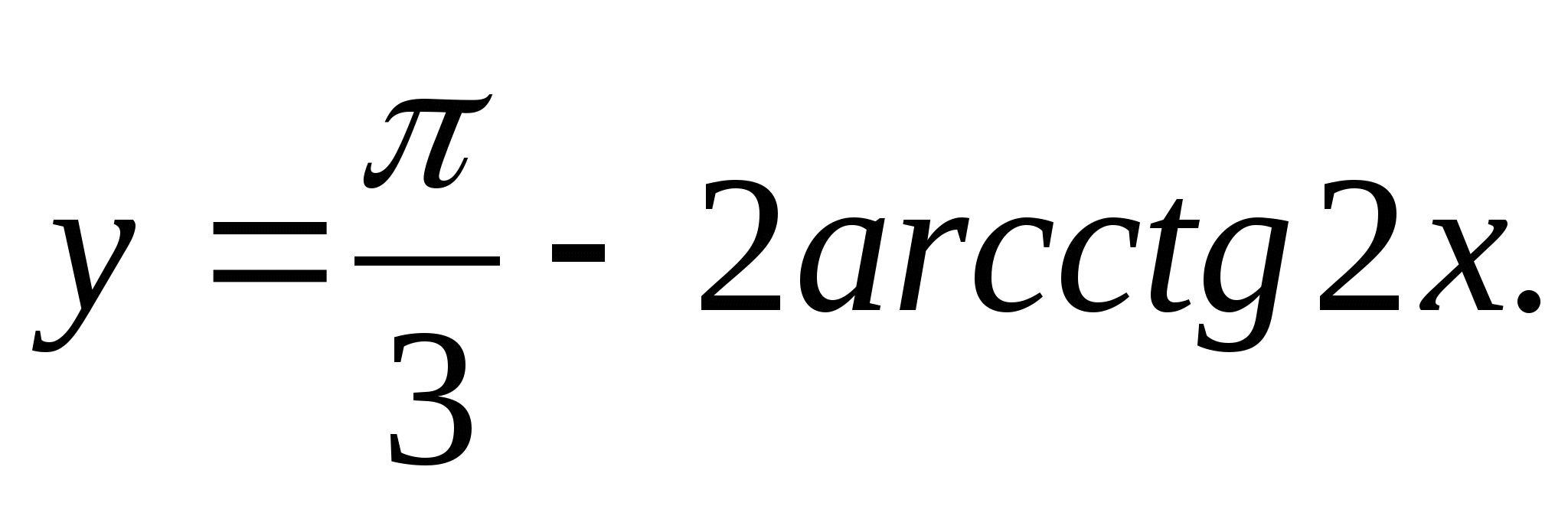




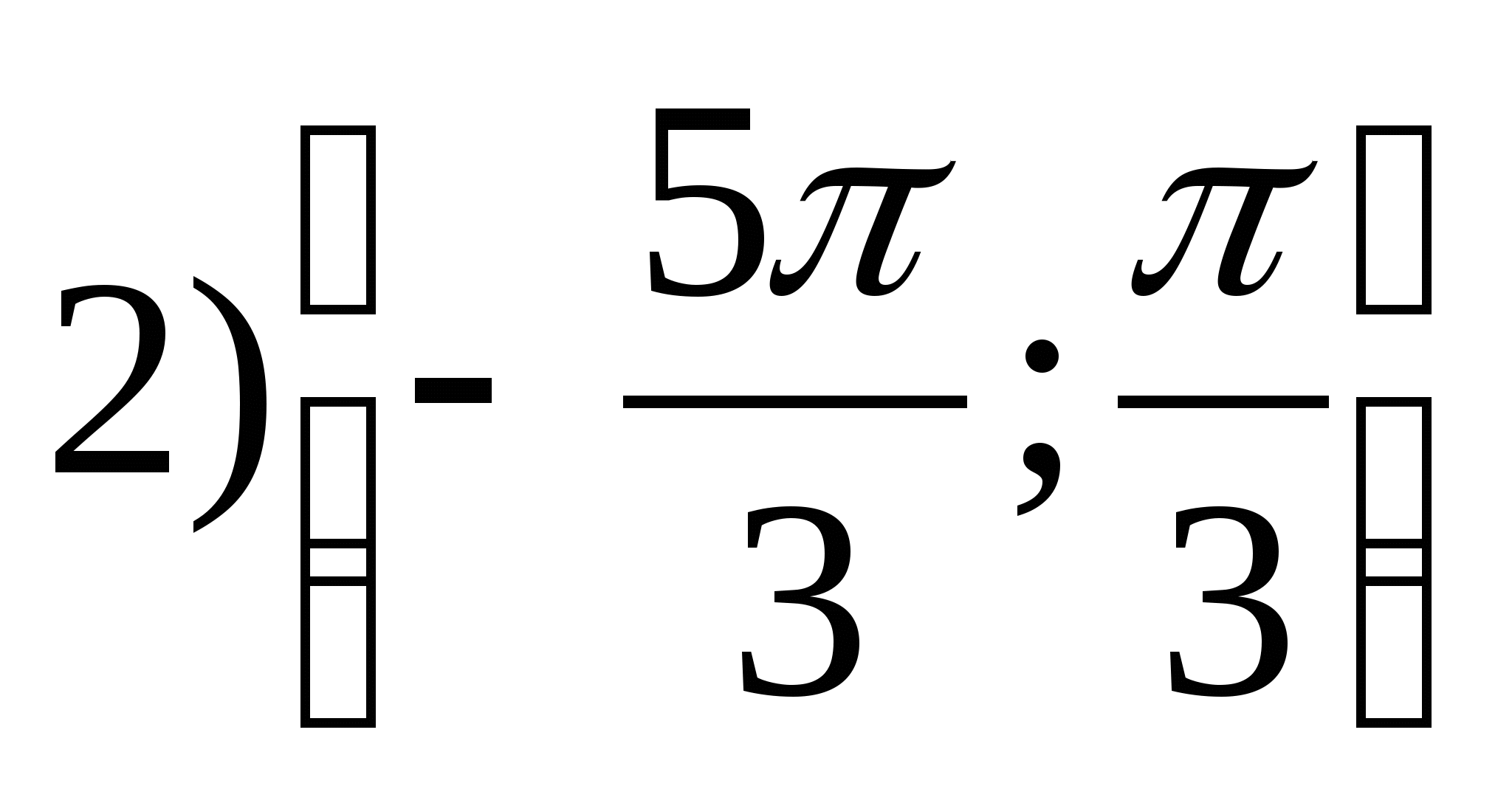
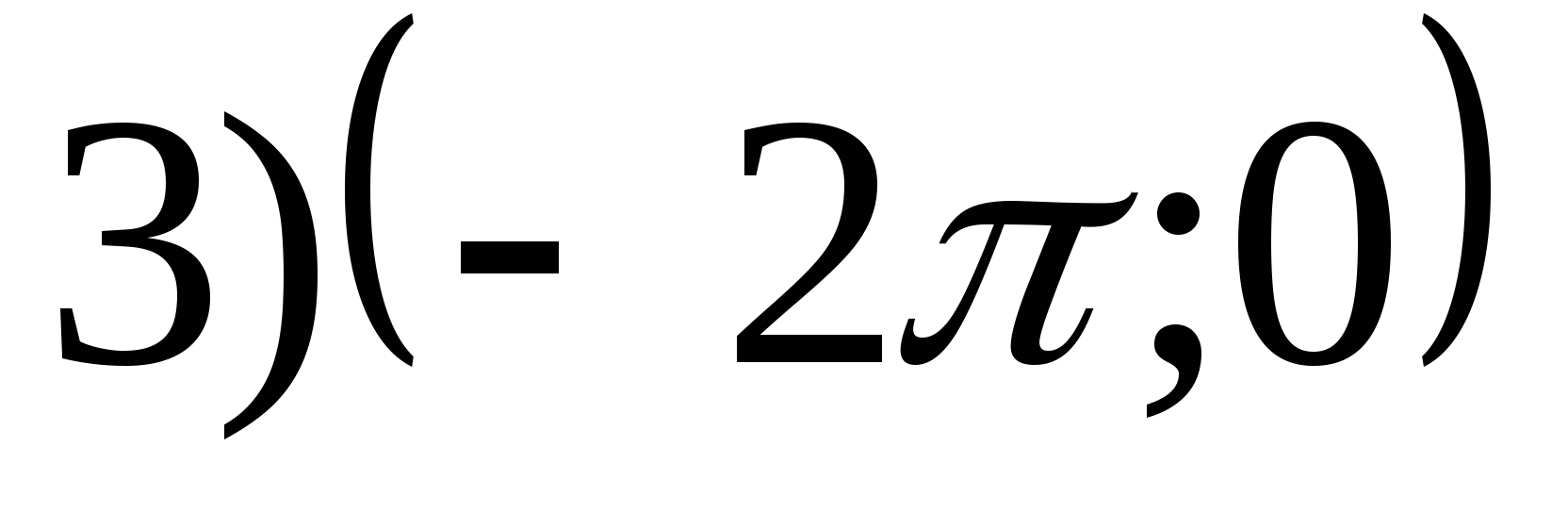
2. Найдите наименьшее значение функции

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Какое из следующих чисел может быть значением функции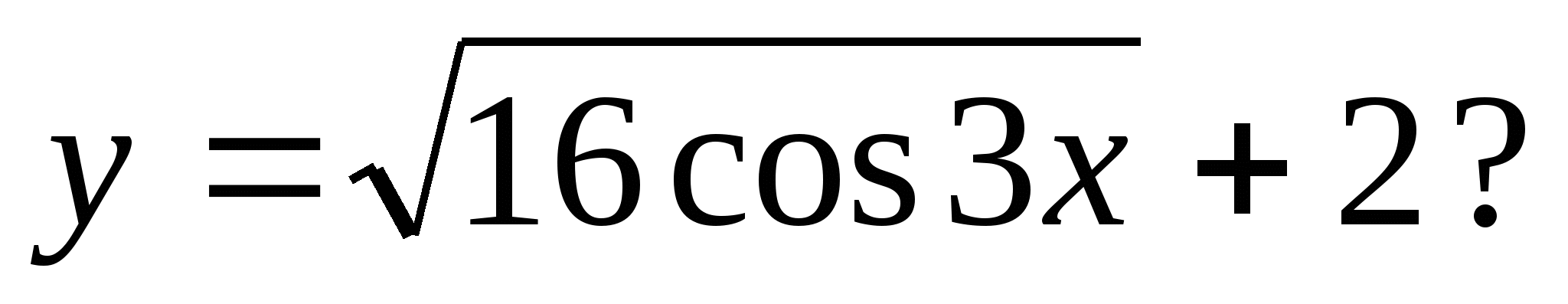

1) -4 2) -1 3) 3 4) 7

4. При каких значениях параметра m уравнение cos (3 x + 2)- m = 5 имеет корни?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Найдите множество значений функции у = -2 ctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Укажите наибольшее значение функции
на промежутке

2) 0 3) 2 4) 1

7. Найдите, сколько целых чисел входит в область значений функции

1) 30 2) 35 3) 17 4) 7

Множество значений показательной и логарифмической функций

Вариант 1

1. Найдите область значений функции

1) 4) (-∞;3)

2. Укажите множество значений функции

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]


1) 0 2) 4 3) -3 4) -4


1) 15 2) 20 3) 43 4) 28


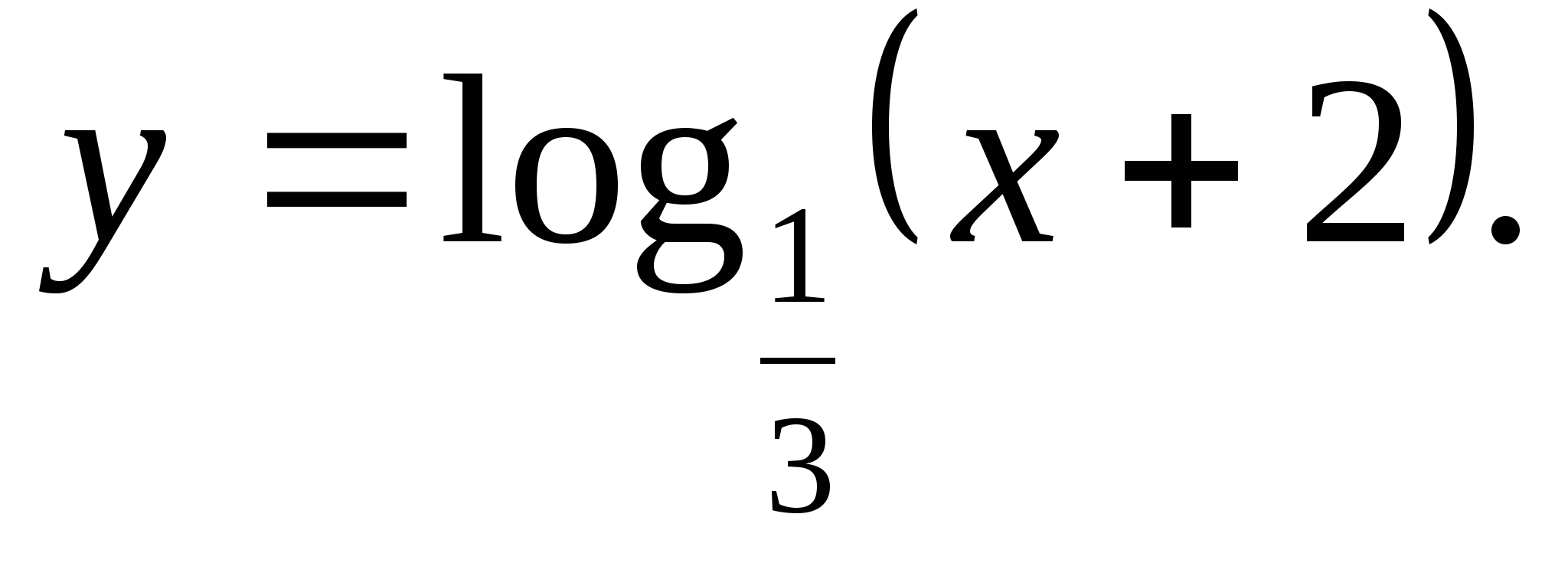
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Укажите наименьшее целое значение функции

1) 1 2) -1 3) 0 4) -5

7. Укажите функцию, множеством значений которой является промежуток (1;∞).


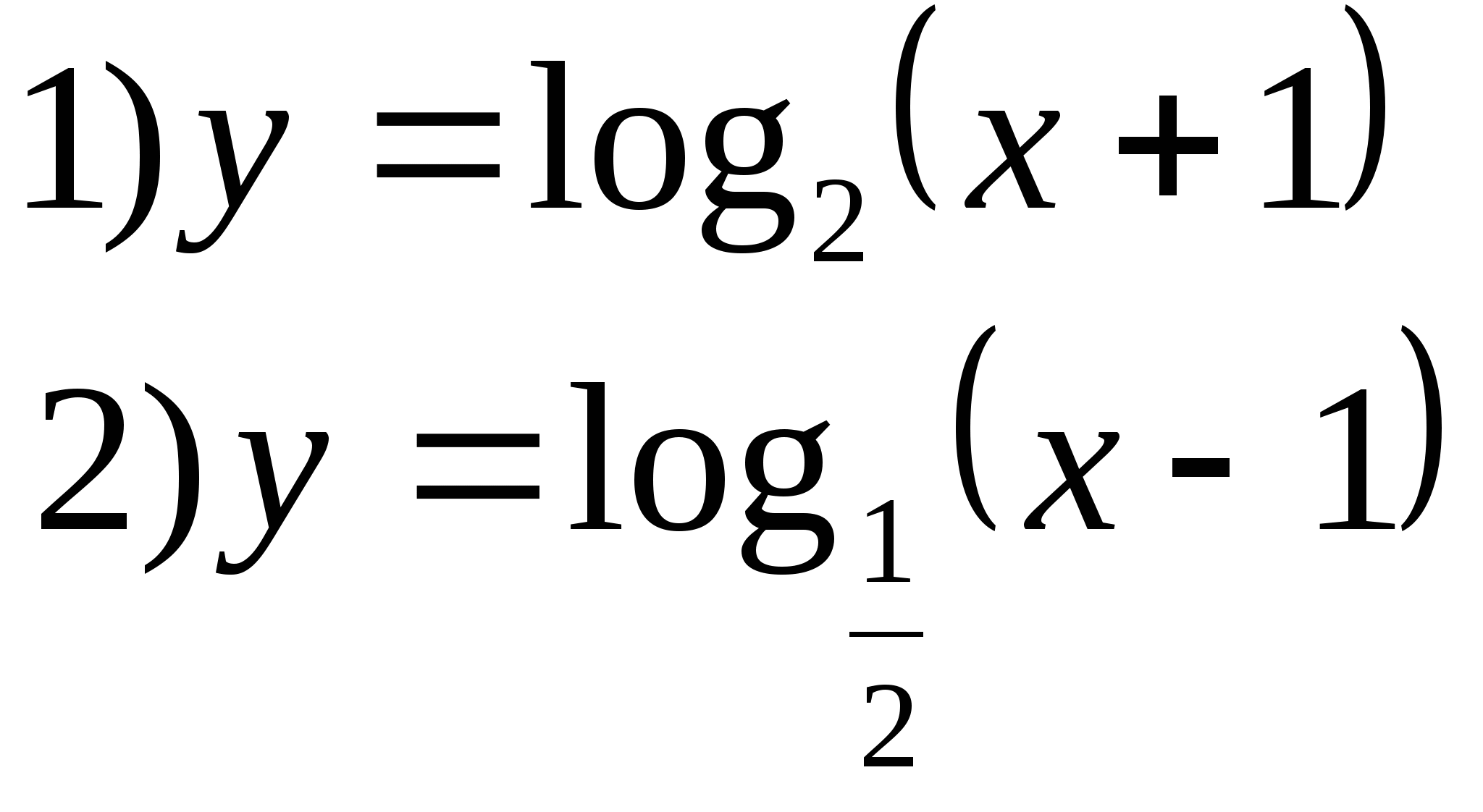
Вариант 2

1. Укажите множество значений функции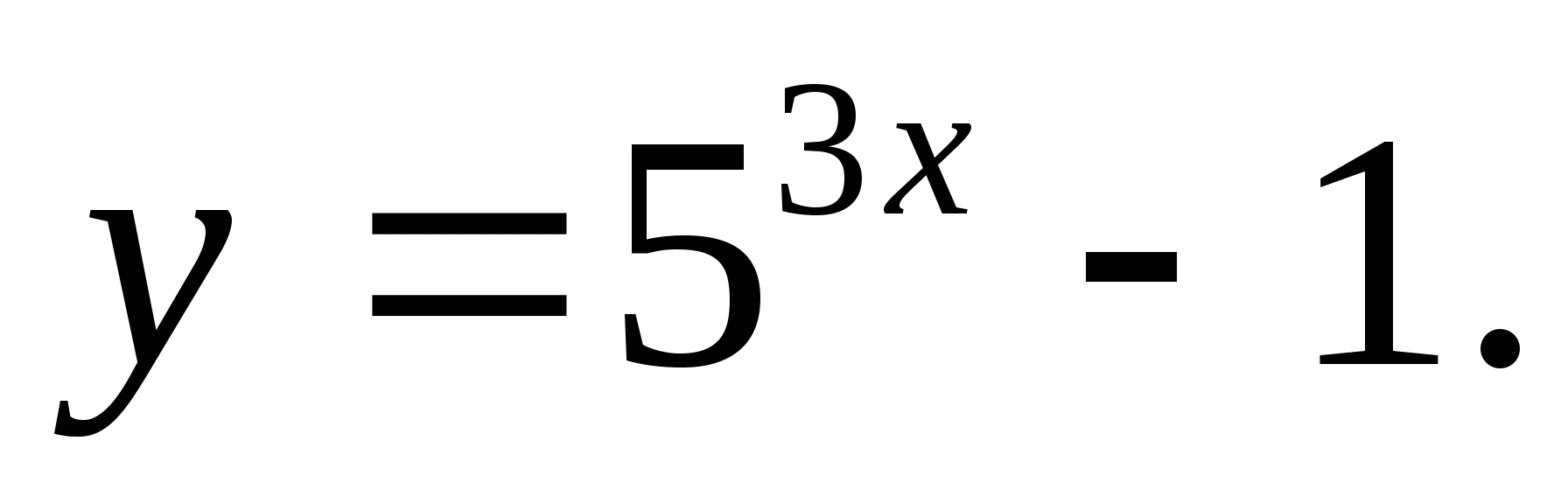

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Найдите область значений функции

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Укажите наименьшее целое значение функции

1) -12 2) -11 3) -10 4) -15

4. Укажите число, не принадлежащее множеству значений фунукции

1) -42 2) 3 3) 1 4) -20

5. Укажите множество значений функции

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Укажите наибольшее целое значение функции

1) 10 2) 3 3) 9 4) 2

7. Укажите функцию, множеством значений которой является промежуток

(-∞;13).


Вариант 5

1. Укажите наименьшее целое значение функции

1) 0 2) -1 3) -2 4) -3

2. Какое из следующих чисел входит в область значений функции

1) -3 2) -4 3) 5 4) 0


1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Найдите, на каком отрезке функция
принимает наибольшее значение, равное 2, и наименьшее значение, равное -3.

1) 2) (-5;2) 3) 4) (-3;2)


на промежутке

1) -1/2 2) 5 3) 2 4) 4

8. Найдите сумму всех натуральных чисел, не входящих в множеств значений функции

1) 3 2) 6 3) 10 4) 8

Вариант 6

1. Укажите наибольшее целое значение функции

1) 2 2) 4 3) 3 4) 5

2. Какое из следующих чисел не входит в область значений функции

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Укажите множество значений функции

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Найдите все точки на ОУ, являющиеся проекциями точек графика функции

1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)

6. Найдите на каком отрезке функция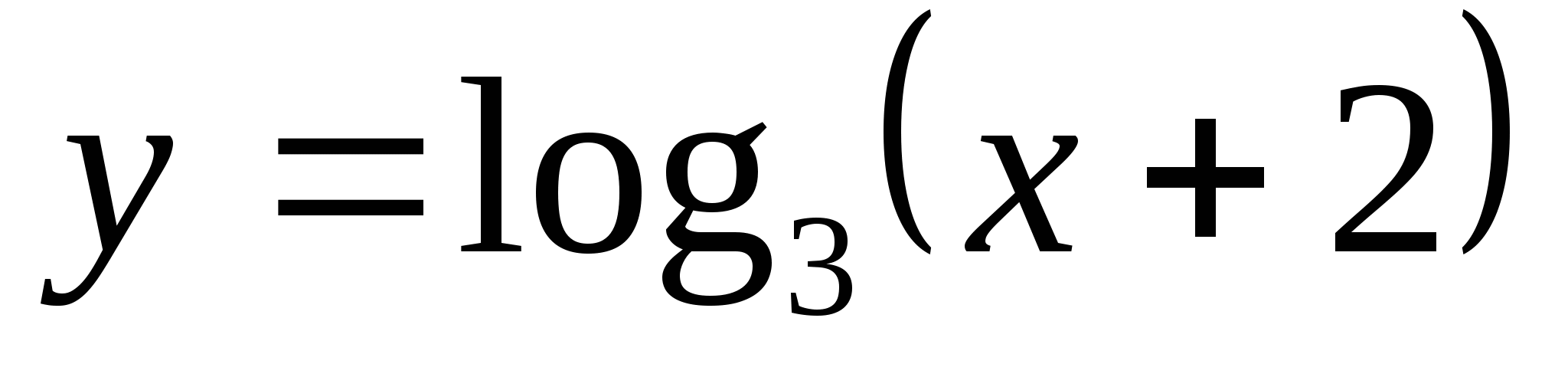
принимает наименьшее значение, равное -2, и наибольшее значение, равное 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Укажите наибольшее значение функции
на промежутке

[-0,9; 0]. 2. Найдите наименьшее значение функции на отрезке .

4. Сколько целых значений принимает функция

Ответы

Часть 1

Множество значений показательной и логарифмической функции

Часть 2

Страница 1
Занятие 3

«Область значений функции»
Цели:- Применять понятие области значений к решению конкретной задачи;

решение типовых задач.

В течение нескольких лет на экзаменах регулярно появляются за­дачи, в которых из данного семейства функций тре­буется выделить те, чьи множества значений удов­летворяют объявленным условиям.

Рассмотрим такого рода задачи.


  1. Актуализация знаний.
Проводится в форме диалога с учащимися.

Что мы понимаем под множеством значений функции?

Как обозначается множество значений функции?


  • По каким данным мы можем найти множество значений функции? (По аналитической записи функции или ее графику)
- Используя рисунок, по графикам найдите область значений функции.

(см задания ЕГЭ, часть А)


  • Множества значений каких функций мы знаем? (Перечисляются основные функции с записью их на доске; для каждой из функций записывается ее множество значений). В результате на доске и в тетради учащихся

Функция

Множество значений

y = x 2

y = x 3

y = | x |

y =


E(y ) =

E(y ) = [- 1, 1]

E(y ) = (– ∞, + ∞)

E(y ) = (– ∞, + ∞)

E(y ) = (– ∞, + ∞)

E(y ) = (0, + ∞)

  • Можем ли мы, используя эти знания, сразу найти множества значений записанных на доске функций? (см. таблицу 2).

  • Что может помочь в ответе на данный вопрос? (Графики этих функций).

  • Как построить график первой функции? (Опустить параболу на 4 единицы вниз).
Аналогично беседуем по каждой функции из таблицы.

Функция

Множество значений

y = x 2 – 4

E(y ) = [-4, + ∞)

y = + 5

E(y ) =

y = – 5 cos x

E(y ) = [- 5, 5]

y = tg (x + / 6) – 1

E(y ) = (– ∞, + ∞)

y = sin (x + / 3) – 2

E(y ) = [- 3, - 1]

y = | x – 1 | + 3

E(y ) =

y = | ctg x |

E(y ) =

y =
= | cos (x + /4) |

E(y ) =

y = (x – 5) 2 + 3

E(y ) = .
Найдите множество значений функции:


.

Введение алгоритма решения задач на нахождение множества значений тригонометрических функций.

Давайте посмотрим, как мы можем применить имеющийся опыт для решения различных заданий, включаемых в варианты единого экзамена.

1. Нахождение значений функций при заданном значении аргумента.

Пример. Найти значение функции у = 2 cos (π/2+ π/4) – 1, если х = - π/2.

Решение.


y (-π/2) = 2 cos (- π/2 – π/4)- 1= 2 cos (π/2 + π/4)- 1 = - 2 sin π/4 – 1 = - 2
– 1 =

= –
– 1.

2.Нахождение области значений тригонометрических функций


Решение.

1≤ sin х ≤ 1

2 ≤ 2 sin х ≤ 2

9 ≤ 11+2sin х ≤ 13

3 ≤
+2∙ sin х ≤
, т.е. Е (у)= .

Выпишем целые значения функции на промежутке . Это число 3.

Ответ: 3.


  • Найдите множество значений функции у = sin 2 х + 6sin х + 10.

  • Найдите множество значений функции: у = sin 2 х - 6 sin х + 8 . (самостоятельно)
Решение.

у = sin 2 х- 2 3 sin х + 3 2 - 3 2 + 8,

у = (sin х- 3) 2 -1.

Е (sin х ) = [-1;1];

Е (sin х -3) = [-4;-2];

Е (sin х -3) 2 = ;

Е (у ) = .

Ответ: .


  • Найдите наименьшее значение функции у = соs 2 x + 2sin x – 2.
Решение.

Можем ли мы найти множество значений этой функции? (Нет.)

Что нужно сделать? (Свести к одной функции.)

Как это сделать? (Использовать формулу cos 2 x = 1-sin 2 x .)

Итак, у = 1-sin 2 x + 2sin x –2,

y = -sin 2 x + 2sin x –1,

у = -(sin x –1) 2 .

Ну, а теперь мы можем найти множество значений и выбрать из них наименьшее.

1 ≤ sin x ≤ 1,

2 ≤ sin x – 1 ≤ 0,

0 ≤ (sin x – 1) 2 ≤ 4,

4 ≤ -(sin x -1) 2 ≤ 0.

Значит, наименьшее значение функции у наим = –4. Ответ: -4.


  • Найдите произведение наибольшего и наименьшего значений функции
у = sin 2 x + cos x + 1,5.

Решение.

у = 1-cos 2 x + cos x + 1,5,

у = -cos 2 x + 2∙0,5∙cos x - 0,25 + 2,75,

у = -(cos x - 0,5) 2 + 2,75.

Е(cos x ) = [-1;1],

Е(cos x – 0,5) = [-1,5;0,5],

Е(cos x – 0,5) 2 = ,

Е(-(cos x -0,5) 2) = [-2,25;0],

Е(у ) = .

Наибольшее значение функции у наиб = 2,75; наименьшее значение у наим = 0,5. Найдём произведение наибольшего и наименьшего значения функции:

у наиб ∙ у наим = 0,5∙2,75 = 1,375.

Ответ: 1,375.



Решение.

Перепишем функцию в виде у =,

у =
,

Найдем теперь множество значений функции.

E(sin x ) = [-1, 1],

E(6sin x ) = [-6, 6],

E(6sin x + 1) = [-5, 7],

E((6sin x + 1) 2) = ,

E(– (6sin x + 1) 2) = [-49, 0],

E(– (6sin x + 1) 2 + 64) = ,

E(y ) = [
, 8].

Найдем сумму целых значений функции: 4 + 5 + 6 + 7 + 8 = 30.

Ответ: 30.



Решение.

1)
то есть х принадлежит I четверти.

2)

Следовательно, 2х принадлежат II четверти.

3) Во II четверти функция синус убывает и непрерывна. Значит, данная функция
принимает все значения от
до

4) Вычислим эти значения:

Ответ:
.




Решение.

1) Так как а синус принимает значения от -1 до 1, то множество значений разности
. При умножении на
этот отрезок перейдет в отрезок
.

2) Арккосинус – монотонно убывающая и непрерывная функция. Значит, множество значений выражения - это отрезок
.

3) При умножении этого отрезка на получим
.

Ответ:
.



Решение.

Так как арктангенс является возрастающей функцией, то
.

2) При возрастании х от
до аргумент 2х возрастает от
до . Так как синус на таком промежутке возрастает, то функция
принимает значения от
до 1.

3) При возрастании от до
аргумент 2х возрастает от до
. Так как синус на таком промежутке убывает, то функция
принимает значения от
до 1.

4) Используя формулу, выражающую синус через тангенс половинного угла, находим, что

.

Значит, искомое множество значений – это объединение отрезков
и
, то есть отрезок
.

Ответ:
.
Данный прием (Введение вспомогательного угла) применяется для нахождения множества значений функций вида

у = a sin x + b cos x или у = a sin (р x) + b cos (р x).


  • Найдите множество значений функции
у = 15 sin 2x + 20 cos 2x.

Решение.

Найдем значение
=
= 25.

Преобразуем выражение

15 sin 2x + 20 cos 2x = 25 (
) = 25 () =

25 sin (2x +), где cos= , sin=.

Множество значений функций у = sin (2x +): -1 sin (2x +) 1.

Тогда множество значений исходной функции -25 25 sin (2x +) 25.

Ответ : [-25; 25].
3. Задания на нахождение наибольшего и наименьшего значения функции на промежутке.


  • Найдите наибольшее и наименьшее значение функции у = сtg х на отрезке [π/4; π/2].
Решение.

Функция у = сtg х является убывающей на отрезке [π/4; π/2], следовательно, наименьшее значение функция будет принимать при х = π/2, то есть у (π/2) = сtg π/2 = 0; а наибольшее значение – при х= π/4, то есть у (π/4) = сtg π/4 = 1.

Ответ: 1, 0.



.
Решение.

Выделим в равенстве
целую часть: .

Отсюда следует, что графиком функции f(x) явля­ется либо гипербола (а≠ 0), либо прямая без точки.

При этом если а; 2а) и (2а;
) и, если а > 0, монотонно возрастает на этих лучах.

Если а = 0, то f(x) = -2 на всей области определе­ния х ≠ 0. Поэтому очевидно, что искомые значения параметра не равняются нулю.

Поскольку нас интересуют значения функции толь­ко на отрезке [-1; 1], то классификация ситуаций определяется тем, что асимптота х = 2а гиперболы (а≠0) располагается относительно этого отрезка.

Случай 1. Все точки промежутка [-1; 1] находят­ся справа от вертикальной асимптоты х = 2а, то есть когда 2а

Случай 2. Вертикальная асимптота пересекает про­межуток [-1; 1], и функция убывает (как и в случае 1), то есть когда

Случай 3. Вертикальная асимптота пересекает про­межуток [-1; 1] и функция возрастает, то есть -1

.

Случай 4. Все точки промежутка [-1; 1] находят­ся слева от вертикальной асимптоты, то есть 1 а > . и второго
Прием 4 . Выражение х через у. (Поиск области определения обратной функции)

Прием 5. Упрощение формулы, задающей дробно-рациональную функцию

Прием 6. Нахождение множества значений квадратичных функций (с помощью нахождения вершины параболы и установления характера поведения её ветвей).

Прием 7. Введение вспомогательного угла для нахождения множества значений некоторых тригонометрических функций.

страница 1

Сегодня на уроке мы обратимся к одному из основных понятий математики - понятию функции; более детально рассмотрим одно из свойств функции - множество ее значений.

Ход урока

Учитель. Решая задачи, мы замечаем, что подчас именно нахождение множества значений функции ставит нас в затруднительные ситуации. Почему? Казалось бы, изучая функцию с 7-го класса, мы знаем о ней достаточно много. Поэтому у нас есть все основания сделать упреждающий ход. Давайте сегодня сами «поиграем» с множеством значений функции, чтобы снять многие вопросы этой темы на предстоящем экзамене.

Множества значений элементарных функций

Учитель. Для начала необходимо повторить графики, уравнения и множества значений основных элементарных функций на всей области определения.

На экран проецируются графики функций: линейной, квадратичной, дробно-рациональной, тригонометрических, показательной и логарифмической, для каждой из них устно определяется множество значений. Обратите внимание учащихся на то, что у линейной функции E(f) = R или одно число, у дробно-линейной

Это наша азбука. Присоединив к ней наши знания о преобразованиях графиков: параллельный перенос, растяжение, сжатие, отражение, мы сможем решить задачи первой части ЕГЭ и даже чуть сложнее. Проверим это.

Самостоятельная работа

Условия задач и системы координат напечатаны для каждого ученика .

1. Найдите множество значений функции на всей области определения:

а) y = 3 sin х ;
б) y = 7 – 2 х ;
в) y = –arccos (x + 5):
г) y = | arctg x |;
д)

2. Найдите множество значений функции y = x 2 на промежутке J , если:

а) J = ;
б) J = [–1; 5).

3. Задайте функцию аналитически (уравнением), если множество ее значений:

1) E (f (x )) = (–∞ ; 2] и f (x ) - функция

а) квадратичная,
б) логарифмическая,
в) показательная;

2) E (f (x )) = R \{7}.

При обсуждении задания 2 самостоятельной работы обратите внимание учащихся на то, что, в случае монотонности и непрерывности функции y = f (x ) на заданном промежутке [a ; b ], множество ее значений - промежуток , концами которого являются значения f (a ) и f (b ).

Варианты ответов к заданию 3.

1.
а) y = –x 2 + 2 , y = –(x + 18) 2 + 2,
y = a (x – x в) 2 + 2 при а < 0.

б) y = –| log 8 x | + 2,

в) y = –| 3 x – 7 | + 2, y = –5 | x | + 3.

2.
а) б)

в) y = 12 – 5x , где x ≠ 1 .

Нахождение множества значений функции с помощью производной

Учитель. В 10-м классе мы знакомились с алгоритмом нахождения экстремумов непрерывной на отрезке функции и отыскания ее множества значений, не опираясь на график функции. Вспомните, как мы это делали? (С помощью производной .) Давайте вспомним этот алгоритм.

1. Убедиться, что функция y = f (x ) определена и непрерывна на отрезке J = [a ; b ].

2. Найти значения функции на концах отрезка: f(a) и f(b).

Замечание . Если мы знаем, что функция непрерывна и монотонна на J , то можно сразу дать ответ: E (f ) = [f (a ); f (b )] или E (f ) = [f (b ); f (а )].

3. Найти производную, а затем критические точки x k J .

4. Найти значения функции в критических точках f (x k ).

5. Сравнить значения функции f (a ), f (b ) и f (x k ), выбрать наибольшее и наименьшее значения функции и дать ответ: E (f )= [f наим; f наиб ].

Задачи на применение данного алгоритма встречаются в вариантах ЕГЭ. Так, например, в 2008 году была предложена такая задача. Вам предстоит решить ее дома .

Задание С1. Найдите наибольшее значение функции

f (x ) = (0,5x + 1) 4 – 50(0,5x + 1) 2

при | x + 1| ≤ 3.

Условия домашних задач распечатаны для каждого ученика .

Нахождение множества значений сложной функции

Учитель. Основную часть нашего урока составят нестандартные задачи, содержащие сложные функции, производные от которых являются очень сложными выражениями. Да и графики этих функций нам неизвестны. Поэтому для решения мы будем использовать определение сложной функции, то есть зависимость между переменными в порядке их вложенности в данную функцию, и оценку их области значений (промежутка изменения их значений). Задачи такого вида встречаются во второй части ЕГЭ. Обратимся к примерам.

Задание 1. Для функций y = f (x ) и y = g (x ) записать сложную функцию y = f (g (x )) и найти ее множество значений:

а) f (x ) = –x 2 + 2x + 3, g (x ) = sin x ;
б) f (x ) = –x 2 + 2x + 3, g (x ) = log 7 x ;
в) g (x ) = x 2 + 1;
г)

Решение. а) Сложная функция имеет вид: y = –sin 2 x + 2sin x + 3.

Вводя промежуточный аргумент t , мы можем записать эту функцию так:

y = –t 2 + 2t + 3, где t = sin x .

У внутренней функции t = sin x аргумент принимает любые значения, а множество ее значений - отрезок [–1; 1].

Таким образом, для внешней функции y = –t 2 +2t + 3 мы узнали промежуток изменения значений ее аргумента t : t [–1; 1]. Обратимся к графику функции y = –t 2 +2t + 3.

Замечаем, что квадратичная функция при t [–1; 1] принимает наименьшее и наибольшее значения на его концах: y наим = y (–1) = 0 и y наиб = y (1) = 4. А так как эта функция непрерывна на отрезке [–1; 1], то она принимает и все значения между ними.

Ответ : y .

б) Композиция этих функций приводит нас к сложной функции которая после введения промежуточного аргумента, может быть представлена так:

y = –t 2 + 2t + 3, где t = log 7 x ,

У функции t = log 7 x

x (0; +∞ ), t (–∞ ; +∞ ).

У функции y = –t 2 + 2t + 3 (см. график) аргумент t принимает любые значения, а сама квадратичная функция принимает все значения не больше 4.

Ответ : y (–∞ ; 4].

в) Сложная функция имеет следующий вид:


Вводя промежуточный аргумент, получаем:

где t = x 2 + 1.

Так как для внутренней функции x R , а t .

Ответ : y (0; 3].

г) Композиция двух данных функций дает нам сложную функцию

которая может быть записана как

Заметим, что

Значит, при

где k Z , t [–1; 0) (0; 1].

Нарисовав график функции видим, что при этих значениях t

y (–∞ ; –4] c ;

б) на всей области определения.

Решение. Вначале исследуем данную функцию на монотонность. Функция t = arcctg x - непрерывная и убывающая на R и множество ее значений (0; π). Функция y = log 5 t определена на промежутке (0; π), непрерывна и возрастает на нем. Значит, данная сложная функция убывает на множестве R . И она, как композиция двух непрерывных функций, будет непрерывна на R .

Решим задачу «а».

Так как функция непрерывна на всей числовой оси, то она непрерывна и на любой ее части, в частности, на данном отрезке. А тогда она на этом отрезке имеет наименьшее и наибольшее значения и принимает все значения между ними:


f (4) = log 5 arcctg 4.

Какое из полученных значений больше? Почему? И каким же будет множество значений?

Ответ:

Решим задачу «б».

Ответ: у (–∞ ; log 5 π) на всей области определения.

Задача с параметром

Теперь попробуем составить и решить несложное уравнение с параметром вида f (x ) = a , где f (x ) - та же функция, что и в задании 4.

Задание 5. Определите количество корней уравнения log 5 (arcctg x ) = а для каждого значения параметра а .

Решение. Как мы уже показали в задании 4, функция у = log 5 (arcctg x ) - убывает и непрерывна на R и принимает значения меньше log 5 π. Этих сведений достаточно, чтобы дать ответ.

Ответ: если а < log 5 π, то уравнение имеет единственный корень;

если а ≥ log 5 π, то корней нет.

Учитель. Сегодня мы рассмотрели задачи, связанные с нахождением множества значений функции. На этом пути мы открыли для себя новый метод решения уравнений и неравенств - метод оценки, поэтому нахождение множества значений функции стало средством решения задач более высокого уровня. При этом мы увидели, как конструируются такие задачи и как свойства монотонности функции облегчают их решение.

И мне хочется надеяться, что та логика, которая связала рассмотренные сегодня задачи, вас поразила или хотя бы удивила. Иначе и быть не может: восхождение на новую вершину никого не оставляет равнодушным! Мы замечаем и ценим красивые картины, скульптуры и т.д. Но и в математике есть своя красота, притягивающая и завораживающая - красота логики. Математики говорят, что красивое решение - это, как правило, правильное решение, и это не просто фраза. Теперь Вам самим предстоит находить такие решения и один из путей к ним мы указали сегодня. Удачи вам! И помните: дорогу осилит идущий!



Похожие статьи